Elektrinio lauko potencialas
Elektrinį lauką apibūdina dvi svarbios charakteristikos: elektrinio lauko stipris ir potencialas. Jau žinome, kad elektrinio lauko stipris yra jėginė lauko charakteristika. Žinodami elektrinio lauko stiprį konkrečiame elektrinio lauko taške, galime apskaičiuoti, kokio didumo jėga elektrinis laukas veikia elektros krūvį tame taške. Norėdami išsiaiškinti antrą elektrinio lauko charakteristiką – potencialą, turime prisiminti, kas yra mechaninė energija. Apie ją mokėtės žemesnėse klasėse.
Kūno kinetinė energija
Žodis „energija“ kilęs iš graikų kalbos žodžio energeia, reiškiančio veikimą. Kas yra energija, suprasti nelengva, nes tiesiogiai jos nepastebime. Nuo energijos dydžio priklauso atliekamas darbas. Žinote, kad judantys kūnai turi kinetinės (gr. kinēma – judėjimas) energijos, kuri žymima simboliu Ek. Kinetinė energija priklauso nuo kūno masės ir greičio. Pavyzdžiui, stebėdami važiuojantį automobilį mes nematome jo kinetinės energijos. Apie ją sprendžiame iš automobilio masės ir greičio. Kuo didesniu greičiu važiuoja automobilis, tuo didesnė jo kinetinė energija, tuo didesnį mechaninį darbą jis gali atlikti įvykus avarijai (išversti medį ar stulpą).
Kūno potencinė energija
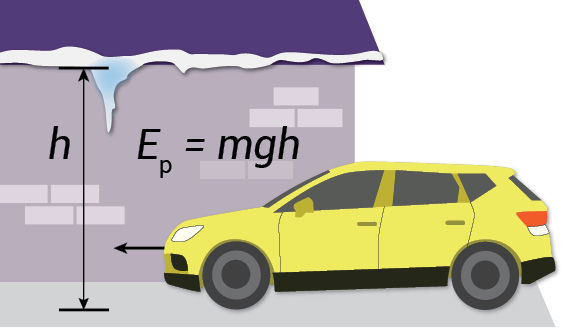
Pakelti nuo žemės arba deformuoti kūnai, pavyzdžiui, ištempta guminė juostelė, spyruoklė, įtemptas lankas, turi potencinės (lot. potentia – jėga, galia) energijos, kuri dar vadinama sąveikos energija. Potencinę energiją įprasta žymėti simboliu Ep. Pavyzdžiui, ant stogo krašto kabantis varveklis turi potencinės energijos. Krisdamas jis gali atlikti mechaninį darbą – sulankstyti automobilio stogą, sužeisti žmogų. Jeigu Žemė varveklio netrauktų, nebūtų sąveikos, atitrūkęs nuo stogo jis nekristų žemyn. Varveklis neturėtų potencinės energijos ir negalėtų atlikti darbo. Kuo didesnė kūno potencinė energija, tuo didesnį darbą jis gali atlikti. Paprastai tariant, kuo didesnis varveklis ir kuo jis aukščiau, tuo daugiau žalos gali padaryti. Fizikos mokslo kalba tą pačią mintį pasakome kitaip: kūno potencinė energija priklauso nuo jo masės (m), pakilimo aukščio (h) pasirinkto paviršiaus atžvilgiu (mūsų atveju – Žemės paviršiaus) ir laisvojo kritimo pagreičio (g) (1.4.1 pav.):
Ep = mgh. (1.3)
Panagrinėkime krintančios žvaigždės potencinę energiją. Krintančios žvaigždės atrodo kaip tolimos ryškios žvaigždės, skriejančios per naktinį dangų (1.4.2 pav.).

Tačiau krintanti žvaigždė visai nėra žvaigždė. Tai įvairaus dydžio kosminių uolienų gabalai, degantys Žemės atmosferoje. Taške A kosminės uolienos gabalas turi didesnę potencinę energiją nei taške B (1.4.2 pav.). Tuo pat metu kūnas gali turėti ir kinetinės, ir potencinės energijos. Pavyzdžiui, krintanti žvaigždė Žemės atžvilgiu turi kinetinės ir potencinės energijos. Kūno kinetinės ir potencinės energijos suma vadinama pilnutinè mechanine energija:
E = Ek + Ep.
Elektros krūvio potencinė energija
Elektros krūvis +q0 erdvėje aplink save sukuria elektrinį lauką (1.4.3 pav.).
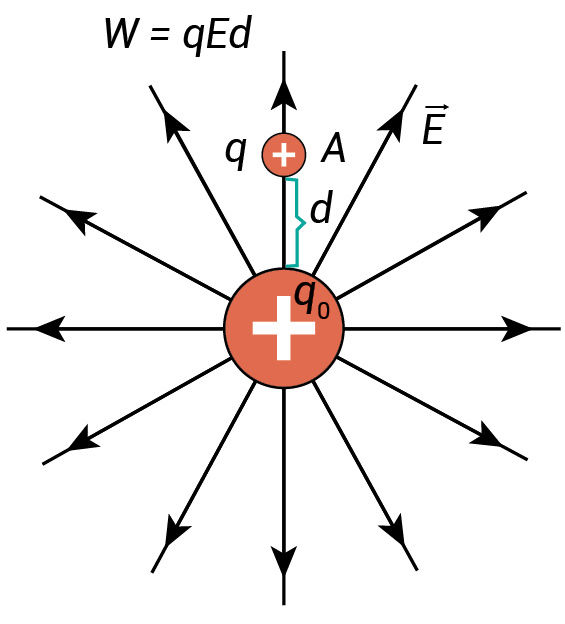
Tarkime, kad šio lauko taške A yra kitas teigiamasis elektros krūvis +q. Šis krūvis įgyja potencinės energijos krūvio +q0 sukurtame elektriniame lauke. Elektros krūvio potencinė energija žymima simboliu W. Ji lygi įnešto krūvio +q didumo, atstumo (d) iki elektrinio lauko šaltinio (krūvio +q0) ir jo sukurto elektrinio lauko stiprio (E) sandaugai:
W = qEd. (1.4)
Kaip ir mechaninė energija, elektros krūvio potencinė energija matuojama džauliais:
[W] = 1 J.
Jei taške A (1.4.3 pav.) būtų dvigubai didesnis elektros krūvis, jo potencinė energija taip pat būtų du kartus didesnė. Vadinasi, skirtingo dydžio elektros krūviai tame pačiame elektrinio lauko taške įgyja nevienodą potencinę energiją.
Elektros krūvio potencinė energija tiriamame elektrinio lauko taške priklauso nuo krūvio ženklo: kai krūvis neigiamasis, ji neigiama, kai teigiamasis – teigiama.
Elektrinio lauko potencialo samprata
Elektros krūvio potencinės energijos (W) ir krūvio (+q) santykis yra pastovus dydis ir nepriklauso nuo krūvio. Vadinasi, jį galime laikyti elektrinio lauko charakteristika. Fizikinis dydis, lygus elektriniame lauke esančio elektros krūvio potencinės energijos ir to krūvio santykiui, vadinamas elektrinio lauko potencialu. Jis paprastai žymimas graikų abėcėlės raide φ (tariama „fi“). Elektrinio lauko potencialas konkrečiame taške išreiškiamas taip:
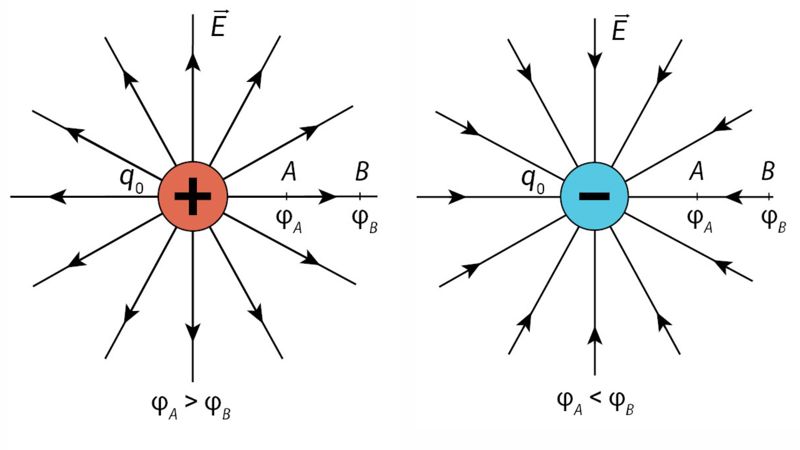
Kaip matyti iš (1.5) formulės, elektrinio lauko potencialas yra lygus elektrinio lauko stiprio (E) konkrečiame taške (pavyzdžiui, A) ir to taško atstumo (d) nuo elektrinio lauko šaltinio sandaugai. Elektrinio lauko potencialas mažėja elektrinio lauko linijų kryptimi (1.4.4 pav.). Tolstant nuo teigiamojo krūvio mažėja, o tolstant nuo neigiamojo didėja.
Elektrinio lauko potencialas – energinė lauko charakteristika
Elektrinio lauko potencialas išreiškia elektrinio lauko pajėgumą. Žinant elektrinio lauko potencialą konkrečiame taške (pavyzdžiui, A arba B) galima nustatyti, kiek potencinės energijos elektros krūvis +q įgytų viename (A) ar kitame (B) elektrinio lauko taške (1.4.4 pav.).
Vadinasi, elektrinio lauko potencialas yra energinė lauko charakteristika. Jis parodo, kiek džaulių energijos įgyja vieno kulono elektros krūvis elektriniame lauke. Jei elektriniame lauke vieno kulono elektros krūvis įgyja vieno džaulio potencinę energiją, elektrinio lauko potencialas prilygsta vienam voltui:
Elektrinio lauko potencialo matavimo vienetas pavadintas voltu (V), pagerbiant italų fiziką Aleksandrą Voltą (Alessandro Giuseppe Volta, 1745–1827), 1800 m. išradusį elektros bateriją.
Klausimai ir užduotys
- Kokia elektrinio lauko potencialo fizikinė prasmė?
- Kokiais vienetais matuojamas elektrinio lauko potencialas?
- Kaip elektros krūvio potencinė energija susijusi su elektrinio lauko potencialu?
- Kaip kinta elektrinio lauko potencialas tolstant nuo jį sukūrusio taškinio teigiamojo krūvio?
- Elektrinio lauko potencialas mažėja iš viršaus į apačią. Į kur nukreiptas elektrinio lauko stipris?
- Judėdamas elektriniame lauke elektronas perėjo į kitą elektrinio lauko tašką, kurio potencialas 1 V didesnis. Kaip pasikeitė elektrono kinetinė energija?
- Taškai A ir B yra vienoje elektrinio lauko linijoje (1.4.5 pav.). Kuriame taške elektrinio lauko potencialas yra didesnis?


