Lygiagretusis laidininkų jungimas

Pramonėje, buityje elektros energijos imtuvai dažniausiai jungiami lygiagrečiai. Pavyzdžiui, namuose taip jungiamos apšvietimo lempos, buitiniai elektriniai prietaisai. Todėl svarbu suprasti lygiagrečiojo laidininkų jungimo dėsningumus.

3.2.1 paveiksle pavaizduotos dvi lygiagrečiai sujungtos lemputės (3.2.1 pav., a) ir šio jungimo būdo elektrinė schema (3.2.1 pav., b).

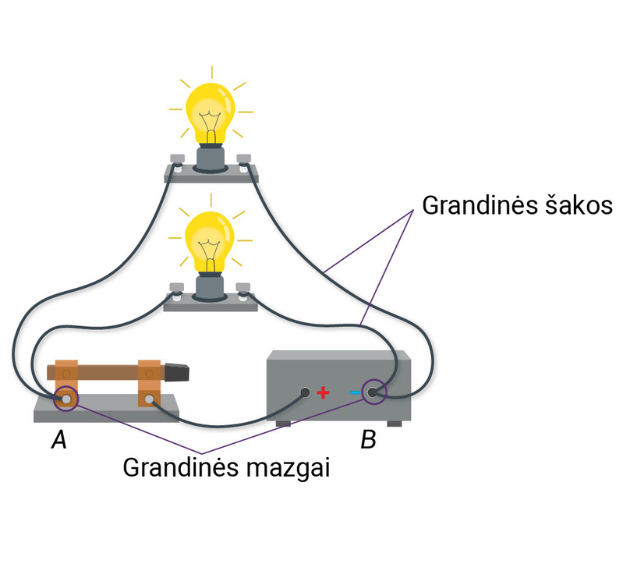
Lygiagrečiojo jungimo atveju vieni laidininkų galai sujungiami kartu viename taške (A), o kiti laidininkų galai sujungiami kartu kitame taške (B) (3.2.1 pav.). Grandinės vieta, kurioje sujungiami daugiau kaip dviejų grandinės elementų gnybtai, vadinama grandinės mazgu. Grandinės (3.2.1 pav.) taškai A ir B yra grandinės mazgai. Lygiagrečiuoju jungimu vadinamas toks jungimo būdas, kai vieni grandinės elementų gnybtai jungiami į vieną mazgą, o kiti į kitą. Visi lygiagrečiai sujungti laidininkai sudaro išsišakojusią dalį, o kiekviena jų vadinama grandinės šaka (3.2.1 pav., a). Išjungus jungiklį elektros srovė nustoja tekėti visomis grandinės šakomis, lemputės užgęsta (3.2.2 pav.).

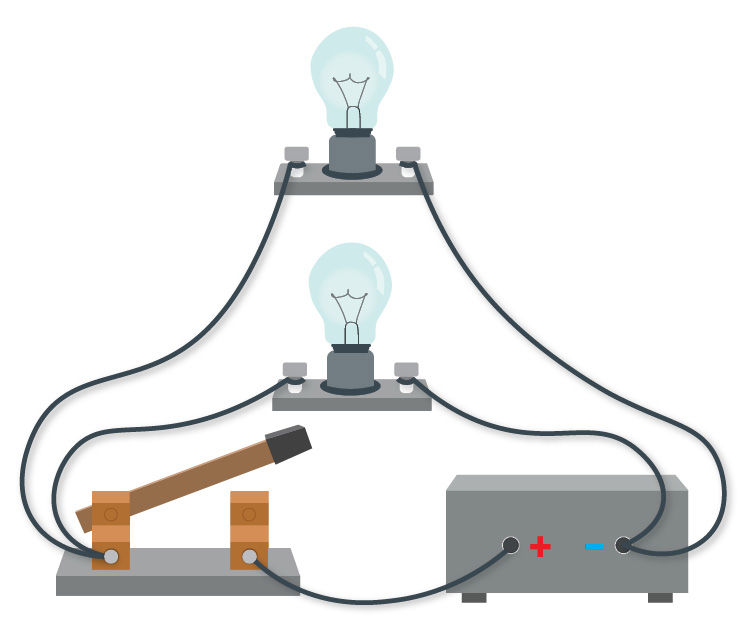
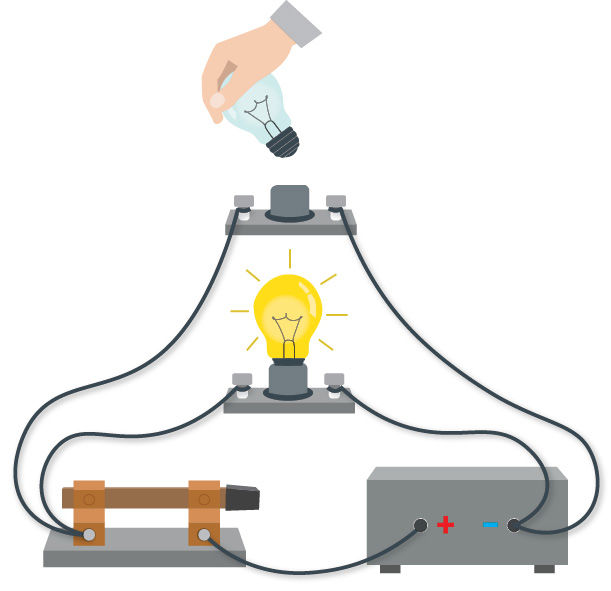
Lygiagrečiojo jungimo atveju atskiromis šakomis tekančios srovės nepriklauso viena nuo kitos. Pavyzdžiui, išsukus vieną elektros lemputę kita lemputė šviečia (3.2.3 pav.).

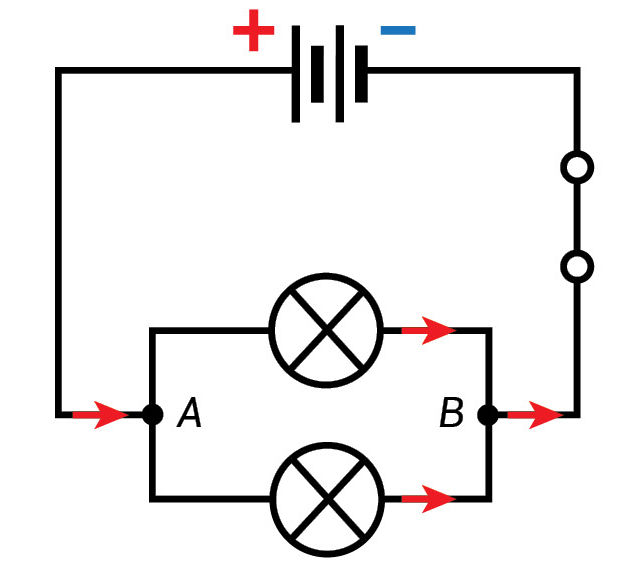
1 taisyklė. Lygiagrečiojo laidininkų jungimo atveju elektros grandinės šakos (1 ir 2) prie srovės šaltinio jungiamos lygiagrečiai (3.2.4 pav., a). Vadinasi, visų lygiagrečiai sujungtų grandinės šakų įtampa yra vienoda:

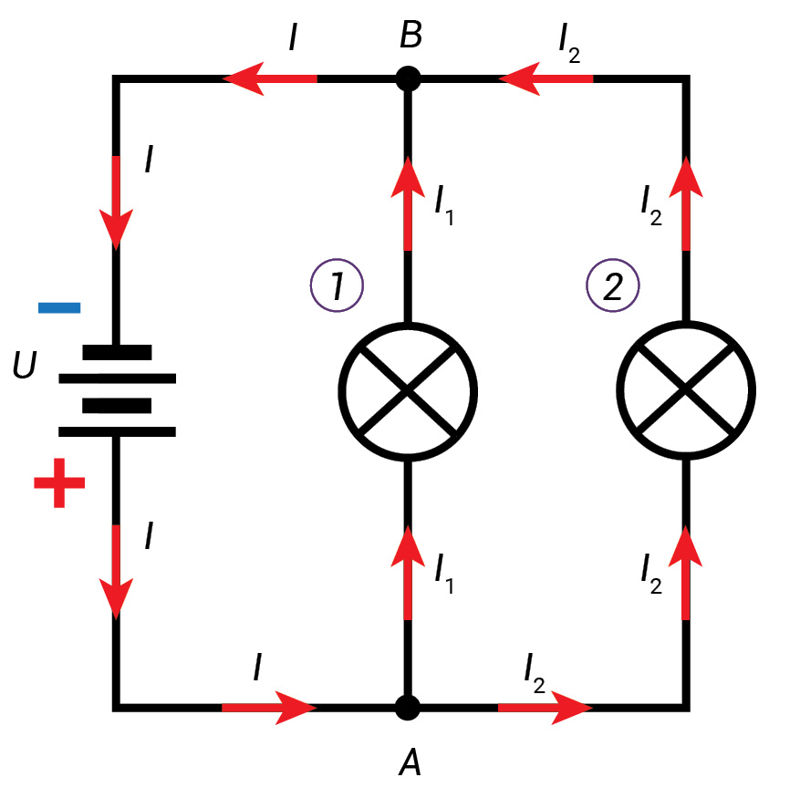
2 taisyklė. Lygiagrečiojo jungimo atveju elektros srovė išsišakoja. Pavyzdžiui, A mazge elektros srovė I išsišakoja į dvi sroves – I₁ ir I₂, o B mazge vėl sudaro bendrą srovę I (3.2.4 pav., a). Taigi, į grandinės mazgą įtekanti srovė (arba įtekančių srovių suma) lygi iš jo ištekančių srovių sumai:

Elektros srovės išsišakojimą galima palyginti su vandens srovės išsišakojimu aplenkiant salą upės vagoje (3.2.4 pav., b).

Iš (3.7) formulės ir Omo dėsnio grandinės daliai išplaukia, kad

\frac{U}{R}=\frac{U}{R_1}+\frac{U}{R_2}.

Abi lygybės puses padaliję iš įtampos U, gauname:

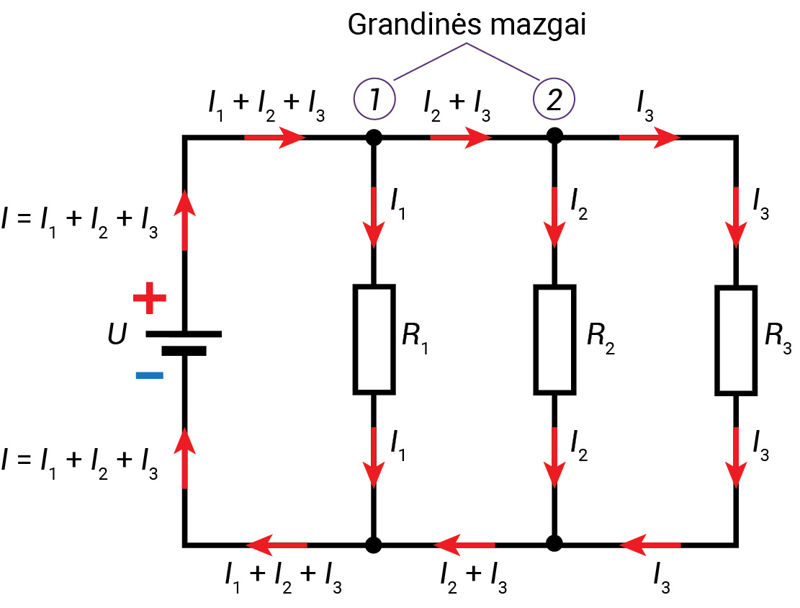
3 taisyklė. Kai laidininkai sujungti lygiagrečiai, fizikinis dydis, atvirkščias pilnutinei grandinės dalies varžai, lygus sumai dydžių, atvirkščių lygiagrečiai sujungtų laidininkų varžoms.

Tarkime, kad lygiagrečiai sujungti du vienodos varžos \left(R_0\right) varžai. Tuomet atvirkščias dydis pilnutinei grandinės varžai lygus:

\frac{\mathrm{1}}{R}=\frac{\mathrm{1}}{R_0}+\frac{\mathrm{1}}{R_0}=\frac{\mathrm{2}}{R_0}\ .

Pilnutinė grandinės varža R lygi:

R=\frac{R_0}{\mathrm{2}}.

Jei lygiagrečiai sujungiama n vienodų varžų, tuomet pilnutinė grandinės varža sumažėja n kartų:

R=\frac{R_0}{\mathrm{2}}. (3 . 9)

Kodėl didinant lygiagrečiai sujungtų varžų skaičių pilnutinė grandinės varža mažėja? Žinoma, kad didinant laidininko skerspjūvį varža mažėja. Kai varžai jungiami lygiagrečiai, tarsi padidėja laidininkų bendras skerspjūvio plotas, o kartu sumažėja varža.

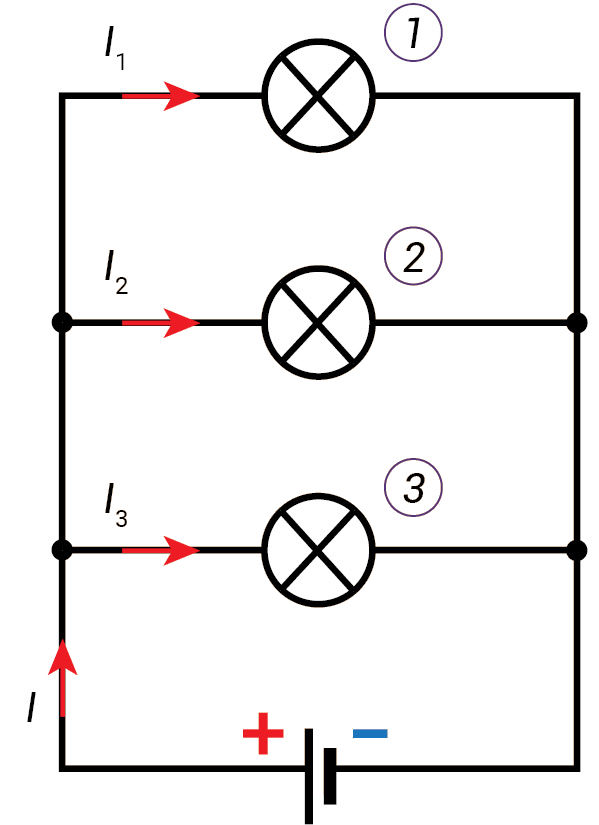
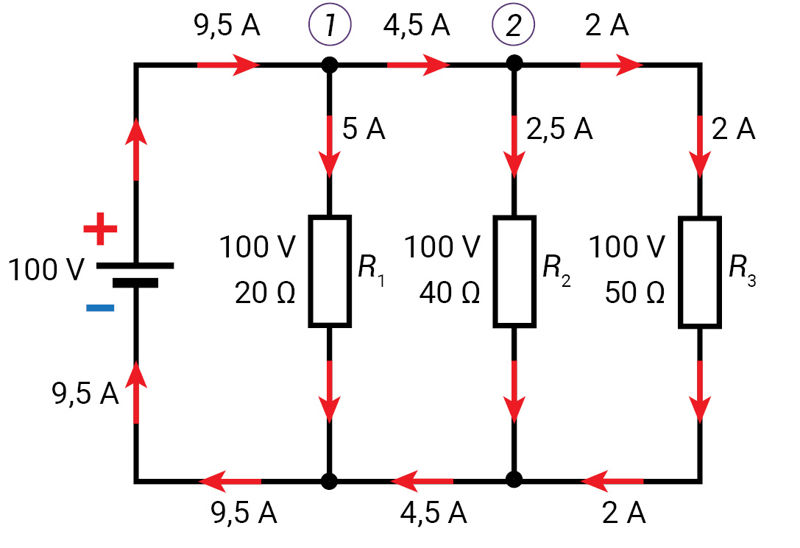
Tarkime, kad elektros grandinę sudaro elektros srovės šaltinis, kurio įtampa 100 V, ir trys lygiagrečiai sujungti varžai: R₁ = 20 Ω, R₂ = 40 Ω, R₃ = 50 Ω (3.2.5 pav., a). Apskaičiuokime: a) elektrinę įtampą varžų gnybtuose (U₁, U₂, U₃); b) pilnutinę grandinės varžą (R); c) srovės stiprį grandinėje (I); d) srovės stiprį grandinės šakose (I₁, I₂, I₃).

1. Lygiagrečiojo jungimo atveju įtampa visų varžų gnybtuose yra vienoda:

U=U_1=U_2=U_3=100\ \mathrm{V}.

1. Remdamiesi (3.8) formule apskaičiuojame pilnutinę grandinės varžą:

\frac{\mathrm{1}}{R}=\frac{1}{20}+\frac{1}{40}+\frac{1}{50};

R=10,5\ \mathrm{\Omega}.

1. Taikome Omo dėsnį ir apskaičiuojame elektros srovės stiprį visoje grandinėje:

I=\frac{100\ \mathrm{V}}{10,5\ \mathrm{\Omega}}=9,5\ \mathrm{A.}

1. Grandinės šakomis teka nevienodo stiprio elektros srovės: I₁, I₂, I₃ (3.2.5 pav., a). Taikome Omo dėsnį ir apskaičiuojame elektros srovės stiprį grandinės šakose:

I_1=\frac{100\ \mathrm{V}}{20\ \mathrm{\Omega}}=5\ \mathrm{A;}

I_2=\frac{100\ \mathrm{V}}{40\ \mathrm{\Omega}}=2,5\ \mathrm{A;}

I_3=\frac{100\ \mathrm{V}}{50\ \mathrm{\Omega}}=2\ \mathrm{A;}

Pirmame grandinės mazge elektros srovė (I) išsišakoja. Dalis jos (5 A) teka pirma grandinės šaka (I₁), o kita dalis (4,5 A) teka link antro grandinės mazgo (3.2.5 pav., b). Antrame grandinės mazge elektros srovė dar kartą išsišakoja. Antra grandinės šaka teka 2,5 A stiprio elektros srovė, o trečiąja – 2 A stiprio elektros srovė (3.2.5 pav., b). Elektros srovės stipris grandinės šakose priklauso nuo varžos: kuo didesnė varža, tuo mažesnis elektros srovės stipris.