Planetų judėjimo dėsniai
SĄVOKOS:
èlipsės židinys, ekscentricitètas, apsidės, afèlis, perihèlis
Planetų judėjimo dėsniai
XVII a. pradžioje vokiečių astronomas ir matematikas Johanesas Kepleris, analizuodamas daugiamečius Marso judėjimo aplink Saulę stebėjimų duomenis, susidūrė su problema. Nuo senovės Graikijos laikų buvo manoma, kad apskritimas yra „tobuliausia“ figūra ir tik jis vienintelis tinka dangaus kūnų judėjimui aprašyti. Bet prie Keplerio turimų duomenų apskritimas nesiderino. Juos Kepleris paveldėjo iš danų astronomo Ticho Brahės, kurio asistentu Kepleris dirbo keletą metų. Nors Brahės stebėjimai atlikti plika akimi, dar iki teleskopo išradimo, bet buvo labai tikslūs ir kruopštūs. Todėl Kepleris atmetė klaidų duomenyse galimybę ir pradėjo ieškoti kitos kreivės Marso orbitai aprašyti. Jo nuostabai, tam geriausiai tiko elipsė. Vėliau paaiškėjo, kad ir kitų planetų orbitos yra elipsės formos. Šis ir dar po kelerių metų ieškojimų atrasti planetų judėjimo dėsniai vėliau buvo pavadinti Kèplerio dėsniais. Jie yra tokie:
- Planeta juda elipsės formos orbita, kurios viename iš židinių yra Saulė (4.1.1 pav.).
Pastaba: iš tiesų viename iš židinių yra Saulės sistemos masės centras, kuris beveik sutampa su Saule (jos masė sudaro 99,86 % Saulės sistemos masės).
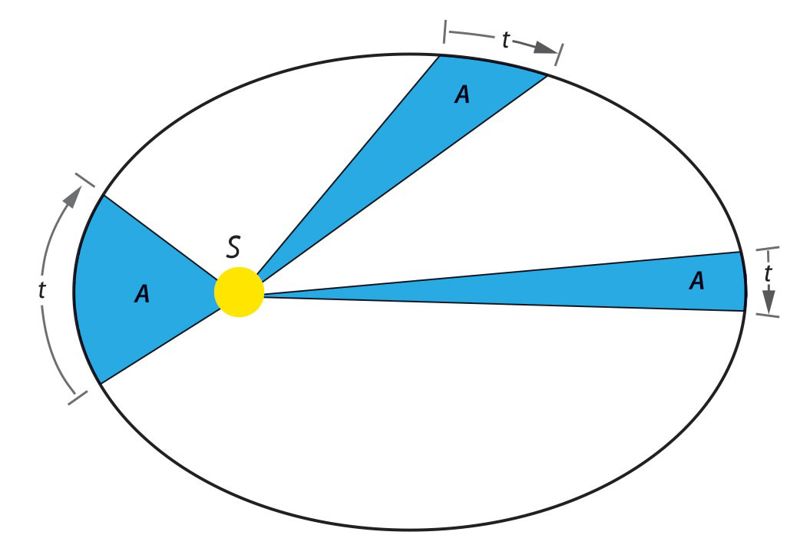
- Spindulys, jungiantis Saulę ir planetą, per vienodus laiko tarpus apibrėžia vienodus plotus.
Matematiškai antrąjį Keplerio dėsnį galima užrašyti taip:
čia A – apibrėžtas plotas; t – laiko tarpas; P – orbitinis periodas; a – didysis pusašis; b – mažasis pusašis; sandauga πab – elipsės plotas.
- Planetų apskriejimo aplink Saulę orbitinių (žvaigždinių) periodų kvadratai proporcingi jų orbitų didžiųjų pusašių kubams.
Matematiškai tai užrašoma taip:
(4.1.2) arba
Saulės atžvilgiu planeta elgiasi panašiai kaip aukštyn kampu nuo žemės mestas kamuoliukas, kurio greitis jam tolstant nuo paviršiaus (analogiškai ir planetai tolstant nuo Saulės) mažėja, o artėjant prie paviršiaus didėja (4.1.2 pav.). Šis panašumas nėra atsitiktinis – tiek kamuoliuko, tiek planetos judėjimą valdo tie patys fizikos dėsniai.
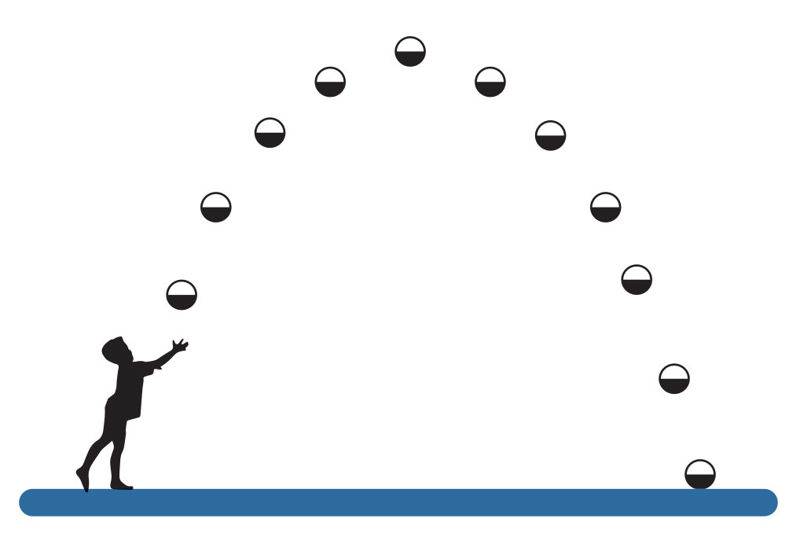
Iš antrojo Keplerio dėsnio išplaukia, kad planeta, skriedama arčiausiai Saulės, juda greičiausiai, o skriedama toliausiai nuo Saulės, juda mažiausiu greičiu Saulės atžvilgiu.
Elipsę galima įsivaizduoti kaip ištemptą apskritimą, kuris turi du židinius F1 ir F2 (4.1.3 pav.). Linija, per centrą jungianti tolimiausius elipsės taškus (apsidès) A1 ir A2, vadinama didžiąja ašimi, o jai statmena B1 ir B2 – mažąja ašimi. Pusė didžiosios ašies vadinama orbitos didžiúoju pùsašiu (|OA1| = |OA2|) ir žymima raide a. Atitinkamai, mažosios ašies pusė (|OB1| = |OB2|) vadinama orbitos mažúoju pùsašiu ir žymima raide b.
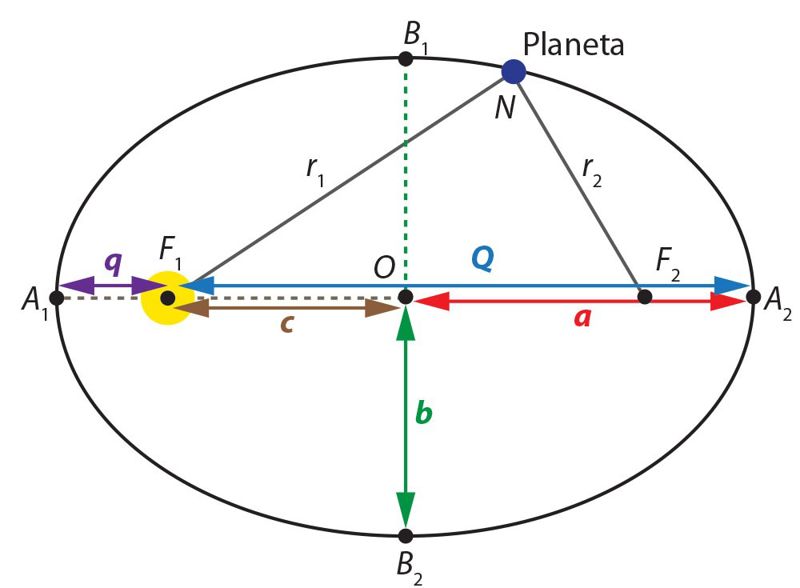
Svarbi elipsės ypatybė: bet kurį jos kreivės tašką N su židiniais jungiančių spindulių ilgių suma lygi didžiosios ašies ilgiui:
|F1N|+|F2N| = |A1A2| = r1 + r2 = 2a. (4.1.4)
Pagal šią ypatybę, naudojantis dviem smeigtukais, virvute ir pieštuku, galima nupiešti elipsę (4.1.4 pav.).

Naudingos formulės
c = ae
b2 = a2(1 – e2)
q = a – ae
Q = a + ae
a = (q + Q)⁄2
Atstumas nuo elipsės centro iki vieno iš židinių |OF1| = |OF2| žymimas raide c. Santykis
Iš trečiojo Keplerio dėsnio (4.1.2) išplaukia, kad dviejų kūnų orbitiniai periodai vienodi, kai jų orbitų didieji pusašiai sutampa. Vadinasi, didysis orbitos pusašis a yra lygus vidutiniam planetos nuotoliui nuo Saulės, t. y. spinduliui apskritimo, kuriuo planeta per laiko tarpą, lygų orbitos periodui P, apskrietų Saulę.
Klausimai ir užduotys
- Kam lygi perihelio ir afelio sumos pusė?
- Kuriame orbitos taške planeta juda greičiau – perihelyje ar afelyje?
- Kaip pasikeis asteroido orbitos didysis pusašis, kai jo orbitinis periodas sutrumpės?
- Planetos orbitinis periodas 163,8 metų. Raskite jos vidutinį atstumą nuo Saulės.
- Įrodykite, kad planeta užtrunka dydžiu
P\frac{e}{\pi} ilgiau (P – orbitos periodas, e – ekscentricitetas) skriedama ketvirtį orbitos pradedant nuo afelio, nei ji praskrietų ketvirtį orbitos pradedant nuo perihelio. - Kokia elipsės savybe remiantis galima nubraižyti elipsę su dviem smeigtukais, virvute ir pieštuku? Tuo remdamiesi nubrėžkite elipsę, kurios ekscentricitetas lygus 0,5. Išmatuokite, kam lygus tokios elipsės apoapsio ir periapsio (tolimiausio ir artimiausio nuo židinio elipsės taško) nuotolių santykis.
