(Astronomija 11–12)

Orbitų trikdžiai

SĄVOKOS:

bariceñtras, apsidžių precèsija

Orbitų trikdžiai

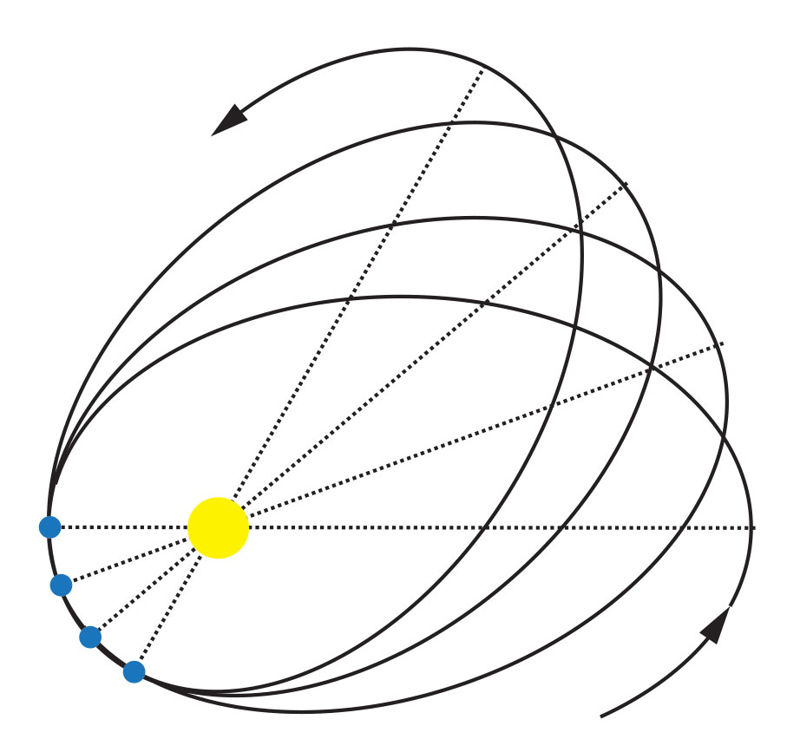
Tiksliai pagal Keplerio dėsnius gali judėti tik du izoliuotą sistemą sudarantys kosminiai kūnai. Tikrovėje egzistuoja daugybė kitų kūnų, kurių gravitacija daro įtaką nagrinėjamo kūno judėjimui. Kuo kiti kūnai arčiau ir kuo didesnė jų masė, tuo trikdymai yra stipresni, o sutrikdytas kūno judėjimas labiau skiriasi nuo nesutrikdyto kūno judėjimo. Saulės sistemoje planetų judėjimo trikdymai nėra labai dideli, nes beveik visa sistemos masė yra sutelkta Saulėje, o planetos skrieja viena nuo kitos palyginti toli. Saulės traukos jėga kiekvienai planetai yra daug kartų didesnė už planetų tarpusavio traukos jėgas, todėl Keplerio dėsniai gana gerai tinka individualiam planetų judėjimui aprašyti. Tačiau situacijose, kai reikia didesnio tikslumo (nustatant tikslias planetų koordinates, kosminiuose skrydžiuose ir pan.), į trikdymus atsižvelgti būtina. Juos įvertinant taikomi kompiuteriniai skaičiavimų metodai. Dėl trikdymų kosminis kūnas gali judėti ne uždara elipse, bet erdvėje orientaciją po truputį keičiančia elipsine kreive (toks reiškinys vadinamas apsidžių precèsija, 4.5.1 pav.), arba elipsę aprašanti kreivė bus vingiuota.

4.5.1 pav. Apsidžių precesija

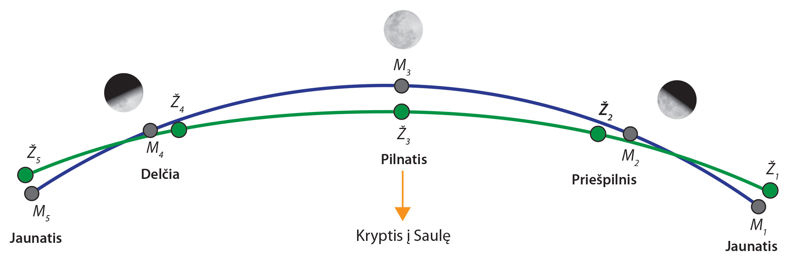
4.5.2 pav. pavaizduotas Žemės (Ž) ir Mėnulio (M) orbitų aplink Saulę fragmentas. Kartu su Žeme judančiam stebėtojui atrodo, kad Mėnulis sukasi aplink Žemę, tačiau iš tiesų Mėnulis, kaip ir Žemė, skrieja aplink Saulę. Žemė yra apie 390 kartų arčiau Mėnulio, bet Saulės masė maždaug 333 000 kartų didesnė, todėl ji traukia Mėnulį apie 2,2 karto stipriau negu Žemė. Dėl savo artumo Žemė sukelia Mėnulio orbitos aplink Saulę trikdžius, kurie pasireiškia ne tik jos vingiavimu, bet ir periodišku Mėnulio greičio kitimu. Žemės traukos jėga suteikia Mėnuliui papildomą pagreitį Saulės atžvilgiu: kai Mėnulis atsilieka nuo Žemės (orbitos taškai M₁–M₂), jis greitinamas, o kai Žemę aplenkia (orbitos taškai M₃–M₄) – lėtinamas. Mėnulio gravitacija taip pat trikdo Žemės orbitą, bet gerokai mažiau, nes Mėnulio masė apie 80 kartų mažesnė už Žemės.

4.5.2 pav. Žemės (Ž) ir Mėnulio (M) orbitų aplink Saulę fragmentas (mastelis padidintas)

Analizuodami kosminių kūnų judėjimo trikdžius astronomai gali ne tik tiksliau nustatyti jų orbitas, bet ir aptikti greta esančius kūnus, kurie vizualiai dar nebuvo pastebėti. Pavyzdžiui, 1846 m., remiantis Urano orbitos trikdymais, atrasta iki tol nežinoma planeta Neptūnas, o 1930 m. jau pagal Neptūno orbitos trikdymus atrasta nykštukinė planeta Plutonas.

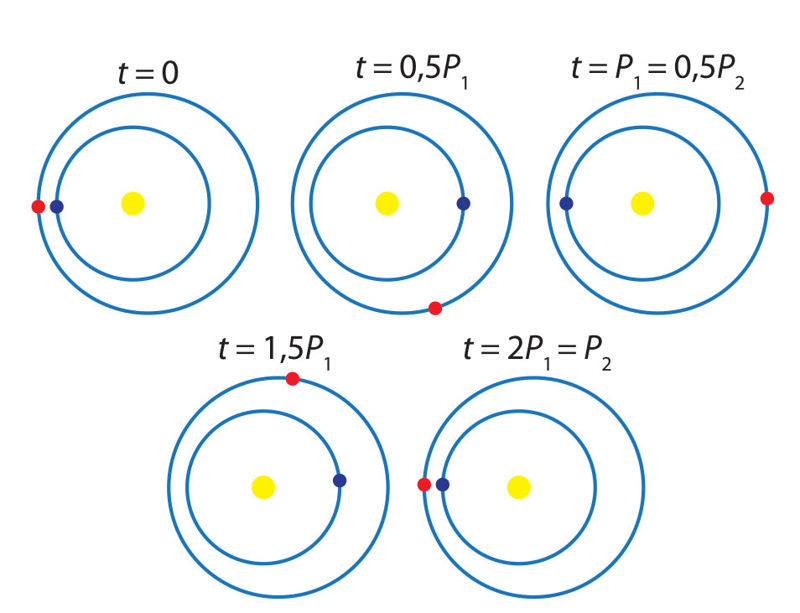
Stipriausius trikdymus Saulės sistemoje sukelia masyviausia planeta Jupiteris – jo masė net 318 kartų didesnė už Žemės. Netoli Jupiterio pralekiančio kūno, pavyzdžiui, kometos, orbita dėl jo gravitacijos poveikio gali tapti tokia, kad kūnas paliks Saulės sistemą arba nuskries į Saulę. Jupiterio masė yra apie 1047 kartus mažesnė už Saulės masę, tačiau jos pakanka, kad šios sistemos masės centras (bariceñtras) atsidurtų už Saulės ribų (4.5.3 pav.).

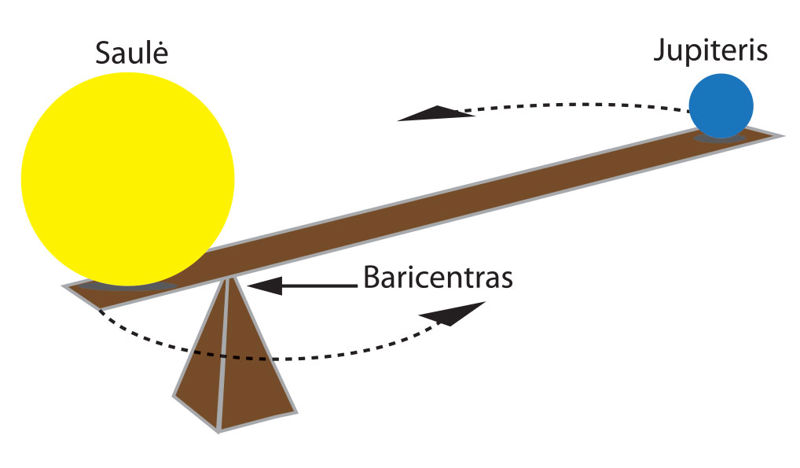
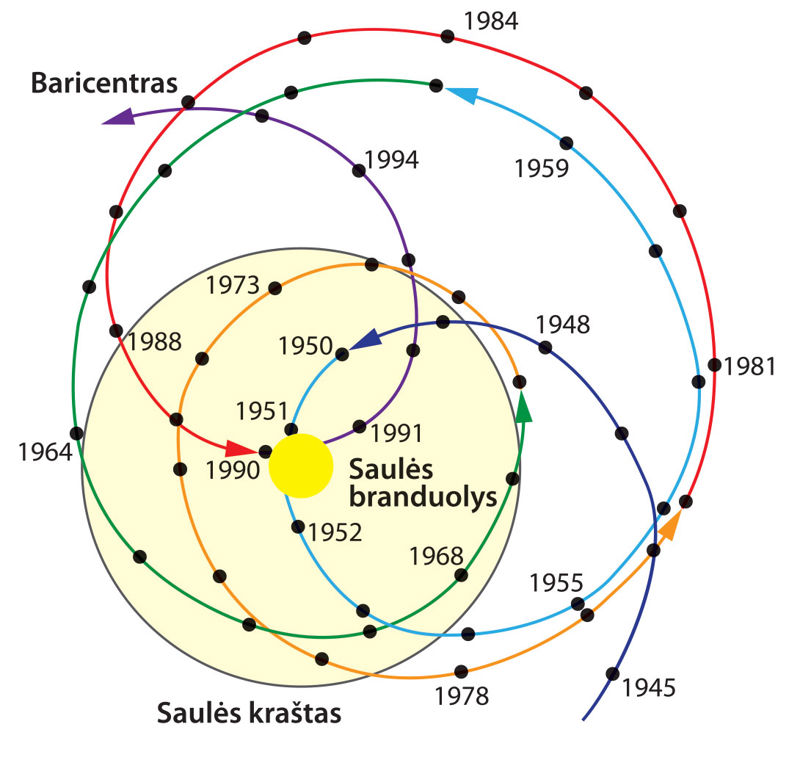
4.5.3 pav. Saulės ir Jupiterio sistemos masės centras

Visi Saulės sistemos kūnai, įskaitant Saulę, juda aplink Saulės sistemos baricentrą. Keičiantis planetų išsidėstymui Saulės atžvilgiu, baricentro padėtis taip pat nuolat kinta (4.5.4 pav.). Be Jupiterio, tam daugiausia įtakos turi antroji pagal masę planeta Saturnas (jo masė apie 3,3 karto mažesnė už Jupiterio).

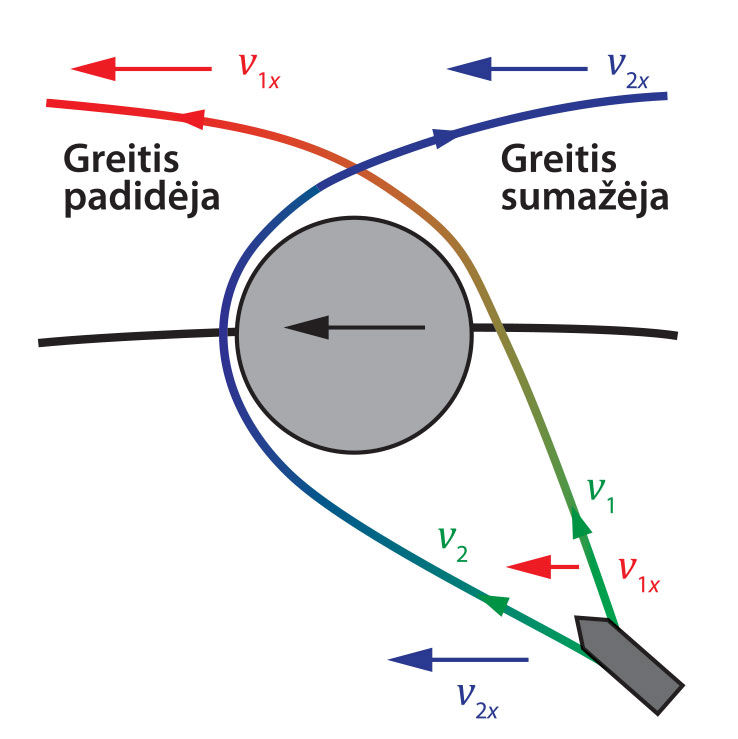
4.5.4 pav. Saulės sistemos baricentro padėties kitimas (skaičiai žymi metus)

Kai dviejų aplink centrinį kūną skriejančių objektų orbitinių periodų santykis gali būti išreikštas nedideliu dviejų sveikųjų skaičių santykiu (2 : 1, 3 : 2, 4 : 3 ir pan.), sakoma, kad tokie objektai skrieja rezonánsinėmis orbitomis (4.5.5 pav.). Kai rezonansinėmis orbitomis skriejantys kūnai prasilenkia nedideliu atstumu, sustiprėja jų tarpusavio gravitacinė sąveika, ir dėl to kiek pakinta jų orbitiniai parametrai. Ilgainiui tokie periodiniai orbitų trikdžiai gali lemti sistemos nestabilumą ir subyrėjimą – kūnai gali susidurti arba pabėgti iš bendros sistemos traukos lauko. Tačiau kai kuriais atvejais kelių kūnų sistema ilgą laiką išlieka stabili kaip tik dėl rezonanso (pvz., Jupiterio didžiųjų palydovų Ganimedo, Europos ir Ijo orbitinių periodų santykis yra 1 : 2 : 4). Kosminių skrydžių metu neretai specialiai suplanuojamas tam tikras orbitos trikdymas – erdvėlaivio trajektorija parenkama tokia, kad skrisdamas pro kosminį kūną jis įgytų reikiamą greitį ir tolesnę judėjimo kryptį (4.5.6 pav.). Tik tokiais gravitaciniais manevrais erdvėlaiviams įmanoma suteikti greitį, leidžiantį ištrūkti iš Saulės sistemos. Pirmasis didesnį už pabėgimo iš Saulės sistemos greitį šiuo būdu įgijo NASA zondas „Pioneer 10“, praskrisdamas pro Jupiterį 1973 m.

4.5.5 pav. Kūnai, kurių žvaigždinių periodų santykis P₁ : P₂ = 2 : 1, skrieja rezonansinėmis orbitomis.

4.5.6 pav. Erdvėlaivio greičio Saulės atžvilgiu pokytis priklauso nuo skrydžio pro kosminį kūną trajektorijos: raudona spalva pažymėta greičio didinimo trajektorija, mėlyna – mažinimo.

N kūnų sistemos baricentro koordinatės apskaičiavimas

N kūnų sistemos baricentro koordinatė c (Dekarto koordinačių sistemoje c yra x, y arba z koordinatė) randama padalijant atskirų kūnų masių m_i ir jų koordinačių c_i sandaugų sumą iš visų kūnų masių m_i sumos:

$c = \frac{\sum_{i = 1}^{N} m_{i} c_{i}}{\sum_{i = 1}^{N} m_{i}} .$

Saulės sistemoje koordinačių atskaitos pradžią patogu susieti su Saulės centru.

Klausimai ir užduotys

Jupiterio masė mažesnė už Saulės 1047 kartus, o Saturno – apie 3500 kartų. Vidutinis Jupiterio orbitos spindulys 5,2 au, o Saturno – 9,6 au. Apskaičiuokite:
1. kokiu atstumu nuo Saulės centro (Saulės spinduliais) yra Saulės, Jupiterio ir Saturno sistemos baricentras, kai Jupiterio atžvilgiu Saturnas yra opozicijoje;
2. kaip pasikeis baricentro vieta Saturnui esant jungtyje su Jupiteriu.
Tos pačios planetos vieno palydovo orbitinis periodas – 88 paros, kito – 110 parų. Ar šių palydovų orbitos rezonansinės? Atsakymą pagrįskite.
Naudodamiesi programėle ištirkite gravitacijos poveikį kosminių kūnų orbitoms. Nustatykite:
1. kokie veiksniai turi įtakos gravitacijos jėgos stiprumui;
2. kaip pasikeičia kūno orbita, jei gravitacija tampa stipresnė arba silpnesnė;
3. kaip nuo kūno greičio (dydžio ir krypties) keičiasi jo orbita;
4. nuo ko priklauso dviejų kūnų sistemos baricentro padėtis;
5. kaip planetos palydovui judant keičiasi jo greitis ir orbita Saulės atžvilgiu;
6. kodėl kinta kometos orbita sistemoje žvaigždė–planeta–kometa;
7. kaip keičiasi zondo greitis ir orbita gravitacinio manevro (angl. slingshot) metu.

Daugiau

Skyriaus „Kosminių kūnų mechanika“ santrauka

Saulės sistemos planetų orbitinį judėjimą nusako Keplerio dėsniai.
Niutono patikslinti Keplerio dėsniai gali būti taikomi bet kokioms gravitaciškai susijusioms dviejų kosminių kūnų sistemoms.
Kosminių kūnų masės gali būti nustatomos remiantis apibendrintu trečiuoju Keplerio dėsniu, kuris susieja stebimus orbitinius dydžius (periodą ir didįjį pusašį) su sistemos kūnų masėmis.
Minimalus greitis, reikalingas, kad objektas apskrietų kosminį kūną apskritimine orbita, kurios spindulys lygus to kūno spinduliui, vadinamas pirmuoju kosminiu greičiu ir apskaičiuojamas taip:\nu_1=\sqrt{\frac{GM}{R}}.
Pabėgimo iš kosminio kūno traukos lauko greitis vadinamas antruoju kosminiu greičiu. Kosminio kūno paviršiuje jis apskaičiuojamas taip: $ν_{2} = \sqrt{2} v_{1}$ .
Taupiausia energijos požiūriu orbitos keitimo trajektorija vadinama Homano orbita.
Visi kūnai, kurie gravitaciškai sąveikauja daugiau kaip su vienu kūnu, patiria judėjimo trikdžius. Jų dydis priklauso nuo sąveikaujančių kūnų masės ir atstumo.