Kaip pakeisti orbitą
Norint iškelti kokį nors objektą (pvz., dirbtinį Žemės palydovą) į orbitą, jam reikia suteikti greitį, ne mažesnį kaip pirmasis kosminis greitis. Keičiant jau skriejančio orbita objekto greitį, keičiasi ir jo orbita. Greitį padidinus pereinama į labiau ištęstą orbitą, o sumažinus – į mažiau ištęstą. Kokia bus naujoji orbita, priklausys ne tik nuo greičio pokyčio, bet ir nuo to, kuriame orbitos taške tai įvyks. Per raketinius skrydžius greitis paprastai keičiamas reaktyviniais varikliais arba pasinaudojant gravitacine sąveika su kokiu nors masyvesniu kosminiu kūnu.
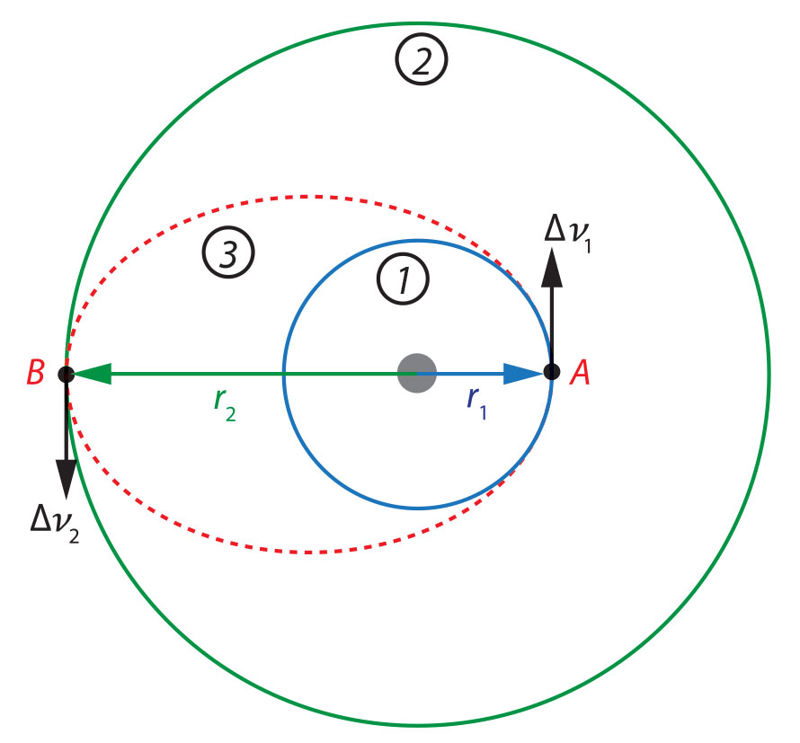
Pati ekonomiškiausia energijos požiūriu perskridimo tarp dviejų orbitų trajektorija vadinama Hòmano (Hohmann) orbità. Tai abi orbitas jungiančios elipsės pusė. Jos pradžia ir atskaitos taškas yra tam tikrame einamosios orbitos taške, o pabaiga (pabaigõs tãškas) – paskirties orbitos taške. Abu šie taškai turi būti priešingose pagrindinio elipsės židinio (sistemos masės centro) pusėse. 4.4.1 pav. pavaizduotas orbitos keitimas iš mažesnio spindulio orbitos r1 į didesnio spindulio orbitą r2. Manevras pradedamas taške A, kuriame raketos greitis padidinamas dydžiu ∆ν1 – tokiu, kad naujasis raketos greitis būtų lygus 3-iąja orbita (elipse) skriejančio kūno greičiui jos periãpsyje (taške A). Įgavusi šį greitį, raketa pradeda skrieti Homano (3-iąja) orbita, kurios didžioji ašis lygi r1+r2. Taške B (apoãpsyje) raketos greitis dar kartą koreguojamas (padidinamas dydžiu Δν2) taip, kad raketos greitis taptų lygus 2-ąja orbita skriejančio kūno greičiui tame taške. Nuo to momento raketa pradeda skrieti šia orbita. Norint perkelti raketą atgal iš 2-osios orbitos į 1-ąją (iš didesnio spindulio orbitos į mažesnio spindulio orbitą), veiksmų seka yra priešinga: pirmiausia sumažinamas greitis taške B (dydžiu Δν2), o paskui – taške A (dydžiu Δν1). Kad Homano orbitos pabaigoje atsidurtų prie paskirties objekto, raketa turi išskristi tam tikrame siaurame laiko intervale, vadinamame skrydžio lángu. Startavusi už jo ribų, raketa su objektu prasilenks – jis bus arba dar neatvykęs, arba jau pasitraukęs iš susitikimui tinkamo orbitos taško. Nustatant tarpplanetinio skrydžio langą, atsižvelgiama į planetų tarpusavio išsidėstymą, taip pat jų orbitinius ir sinodinius periodus.
Kosminio kūno greitis orbitoje gali pakisti jam prasilenkiant (žr. 4.5.6 pav.) arba susiduriant su kitu kūnu. Fizikinis to pagrindas – jùdesio kiekio tvermės dėsnis. 2022 m., atliekant DART (4.4.2 pav.) eksperimentą, NASA zondas dideliu greičiu smogė į nedidelį Dimorfo (Dimorphos) asteroidą – dėl to jo orbitos periodas aplink didesnį Didimo (Didymos) asteroidą sutrumpėjo 32 minutėmis.

Per ilgą laiką asteroido orbita gali šiek tiek pasikeisti ir dėl nevienodos visomis kryptimis nuo jo paviršiaus sklindančios spinduliuotės, nes labiau įkaitusį arba daugiau šviesos atspindintį asteroido šoną veikia papildoma stūmos jėga.
Klausimai ir užduotys
- Kaip reikia pakeisti raketos greitį, kai ją reikia perkelti į mažesnio spindulio orbitą, ir kaip, kai perskrendama į didesnio spindulio orbitą?
- Aprašykite skrydžio seką, kaip erdvėlaivis su mažiausiomis energijos sąnaudomis nuskries:
- iš Žemės orbitos iki Veneros ir liks skrieti Veneros orbita;
- iš Žemės orbitos iki Marso ir liks skrieti Marso orbita.
Judesio kiekio tvermės dėsnis
Kai mes einame, atsispiriame nuo žemės, kai plaukiame, – nuo vandens. Lėktuvai skrenda, nes, sparnui skrodžiant orą, dėl jo formos atsiranda keliamoji jėga. Beorėje erdvėje nėra nuo ko „atsispirti“. Tačiau ten esantys erdvėlaiviai vis tiek sugeba manevruoti, keisti greitį ir orbitą. Kaip tai įmanoma? Atsakymas – jùdesio kiẽkio tvermės dėsnis, kurį pirmasis suformulavo prancūzų filosofas, matematikas ir fizikas Renė Dekartas (René Descartes, 1596–1650), o teoriškai pagrindė Izaokas Niutonas remdamasis antruoju ir trečiuoju jo vardu pavadintais dėsniais.
Judesio kiekiu p vadinama kūno masės ir greičio sandauga – tai vektorinis dydis (
Raketai skriejant orbita išjungtais varikliais, jos nešamo kuro ir likusios raketos masės judesio kiekių suma atskaitos sistemoje, susietoje su raketa, yra lygi nuliui (nes abiejų komponentų greičiai raketos atžvilgiu lygūs nuliui). Kai raketos varikliai įjungiami, iš jos besiveržiančių dujų srauto ir likusios raketos masės judesio kiekių suma ir toliau turi likti lygi nuliui. Jei dujos lekia priešinga kryptimi, negu juda raketa, jų greičių vektoriai yra priešingos krypties, todėl
čia mr ir Δvr – raketos masė ir jos greičio pokytis, o md ir vd – išmetamų per sekundę dujų masė ir jų greitis raketos atžvilgiu (išmetimo greitis).
Iš to išplaukia, kad raketos greičio pokytis
Tipinis dujų išmetimo greitis raketose siekia 3–4 km/s, tačiau dėl išmetamų dujų santykinai mažos masės raketos greitis per vieną trumpą pliūpsnį pakinta labai nedaug. Didesnis pokytis pasiekiamas, kai pliūpsnis trunka ilgiau arba atliekama trumpų pliūpsnių serija. Pažymėtina, kad per kiekvieną kitą pliūpsnį greičio pokytis šiek tiek padidėja, nes senkant kurui mažėja raketos masė, t. y. didėja santykis
* * *
Pritaikykime judesio kiekio tvermės dėsnį kosminių kūnų susidūrimo atvejui. Tarkime, kad į asteroidą, kurio masė M ir greitis νM, greičiu νm smogia m masės meteoritas ir jame lieka. Kadangi bendras judesio kiekis prieš smūgį ir po jo nesikeičia, tai
Asteroido greitis po smūgio
Tarkime, kad atskaitos sistema susieta su asteroidu (t. y. νM = 0), tada po smūgio asteroido greičio pokyčio projekcijos X ir Y ašyse bus:
čia νmx – meteorito greičio asteroido atžvilgiu projekcija X ašyje, o νmy – projekcija Y ašyje (jei ji teigiama, asteroido greitis padidėja, o jei neigiama, sumažėja).
Visas greičio pokytis (4.5.7)
Jei meteorito greitis asteroido atžvilgiu 50 km/s, o jo masė 100 000 kartų mažesnė už asteroido masę, tai tokio meteorito smūgis kaktomuša asteroido greitį sumažintų 0,5 m/s.
