Mišriojo laidininkų jungimo samprata
Sodai – geometrinės formos dirbiniai, dažniausiai gaminami iš šiaudų (3.3.1 pav.). Pinant sodą šiaudai veriami ant siūlo ir surišami į mazgus. Jei šiaudus tapatintume su elektros srovės imtuvais (varžu, lempute), o jų sujungimo vietą su elektros grandinės mazgu, šiaudiniuose soduose galėtume įžvelgti nuosekliojo ir lygiagrečiojo jungimo atvejus (3.2.1 pav.). Jungimo būdas, kai derinami nuoseklusis ir lygiagretusis laidininkų jungimo būdai, vadinamas mišriuoju jungimu. Šiam jungimo būdui taikomos tos pačios nuosekliojo ir lygiagrečiojo laidininkų jungimo taisyklės. Tačiau, norint pritaikyti tas taisykles, pirmiausia reikia išsiaiškinti, kurios elektros grandinės dalys sujungtos nuosekliai, o kurios lygiagrečiai. Tai vadinama mišriojo laidininkų jungimo grandinės supaprastinimu.

Mišriojo laidininkų jungimo nagrinėjimo pavyzdys
Vienoje schemoje (3.3.2 pav., a) pavaizduotas mišrusis laidininkų jungimo būdas, kitoje (3.3.2 pav., b) – varžų skaitinės vertės ir šaltinio įtampa (15 V). Pasimokykime apskaičiuoti pilnutinę grandinės varžą ir elektros srovės stiprį kiekviename varže.
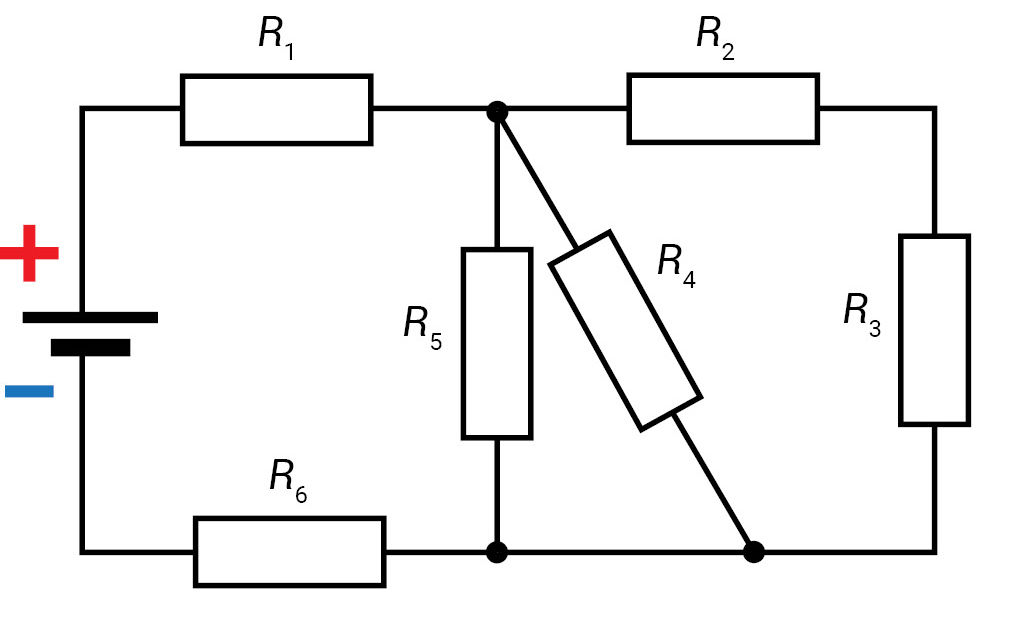
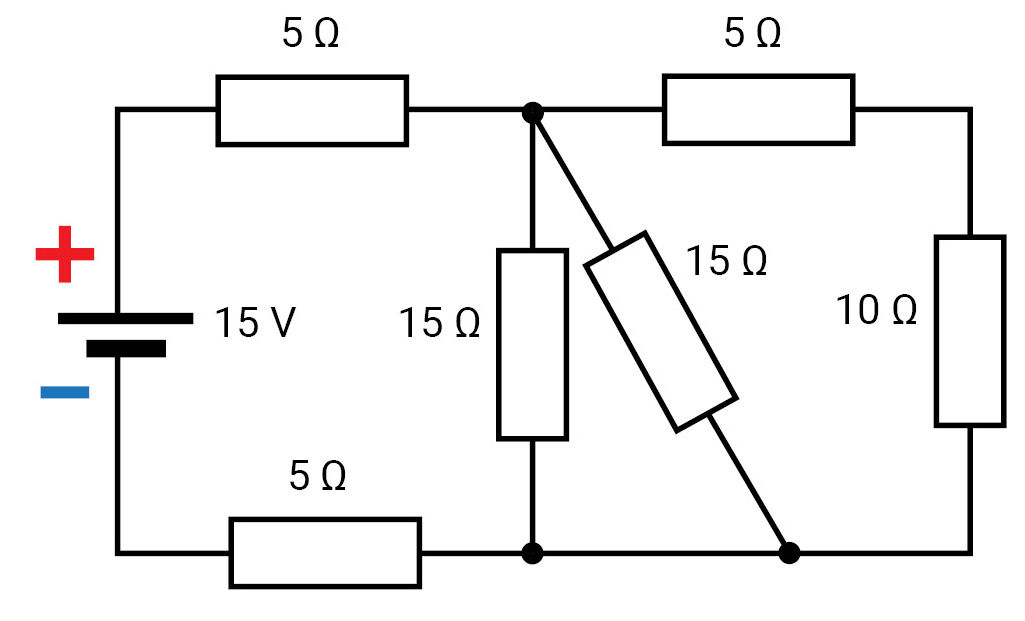
1 grandinės supaprastinimo etapas. Supaprastinkime pirminę elektros grandinės schemą (3.3.2 pav., a). Iš jos matyti, kad varžai R2 ir R3 sujungti nuosekliai. Apskaičiuojame jų bendrą varžą:
Varžai R4 ir R5 tarpusavyje sujungti lygiagrečiai ir prie jų lygiagrečiai prijungta grandinės šaka su varžais R2 ir R3. Pirminę schemą supaprastiname ir gauname antrinę schemą (3.3.3 pav., a). Kadangi trys vienodi varžai (R23 = R4 = R5 = 15 Ω) (3.3.3 pav., b) sujungti lygiagrečiai, jų bendrą varžą (R2345) randame taip:
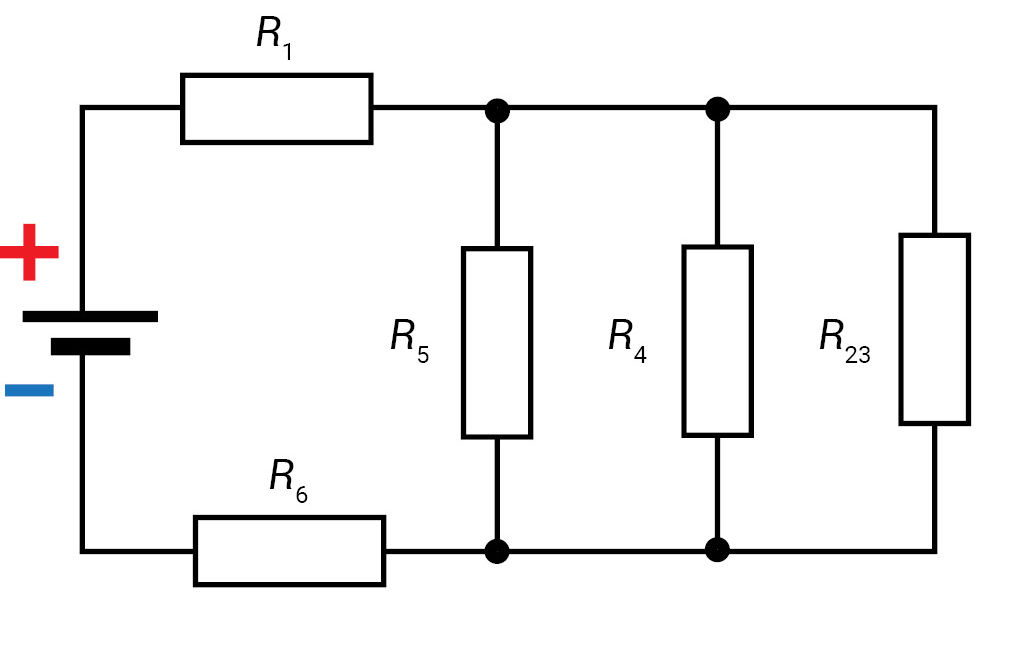
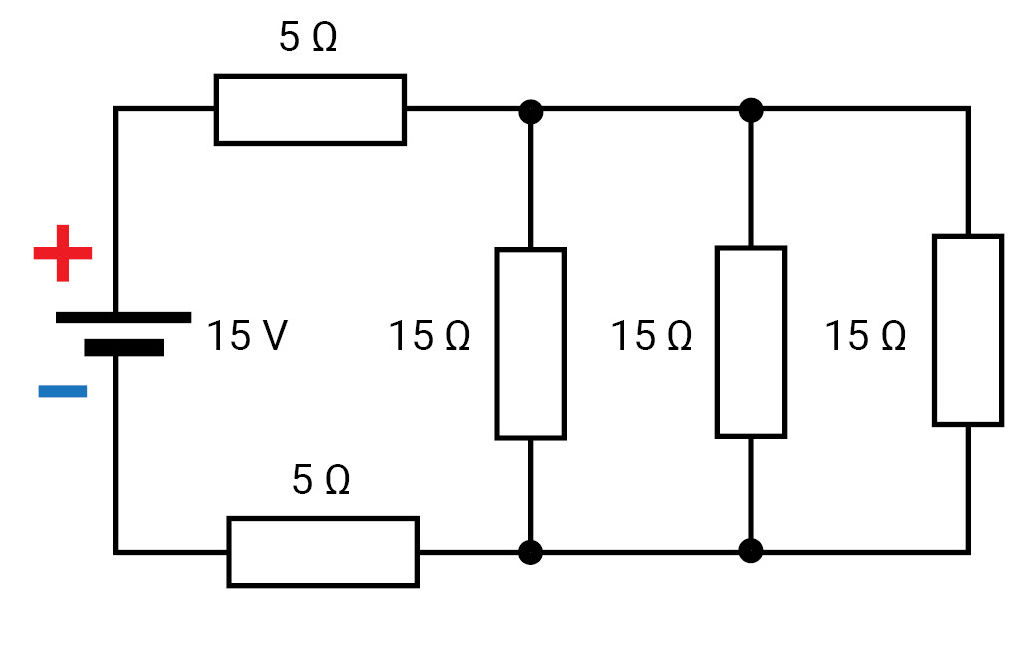
2 grandinės supaprastinimo etapas. Antrinę schemą (3.3.3 pav., a) supaprastiname ir gauname trečią schemą (3.3.4 pav.). Iš jos apskaičiuojame pilnutinę visos grandinės varžą:
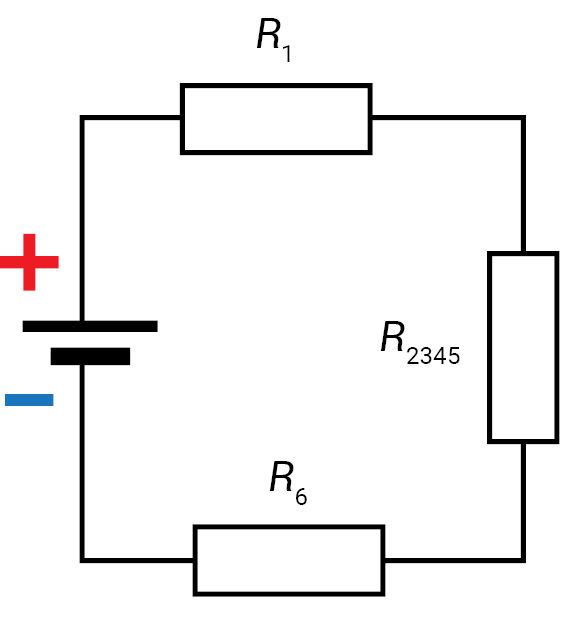
Omo dėsnio taikymas. Taikome Omo dėsnį ir apskaičiuojame elektros srovės stiprį nešakotinėje grandinės dalyje:
Vadinasi, per pirmą ir šeštą varžą teka 1 A stiprio elektros srovė (3.3.2 pav., a).
Iš antrinės schemos (3.3.3 pav., a ir b) akivaizdu, kad lygiagrečiai sujungtoje grandinės dalyje elektros srovė išsišakoja į tris šakas. Kadangi visų grandinės šakų varžos vienodos, jomis tekės tris kartus mažesnio stiprio elektros srovės nei nešakotinėje grandinės dalyje:
Antras (R2 = 5 Ω) ir trečias (R3 = 10 Ω) varžai sujungti nuosekliai, per juos teka vienodo stiprio elektros srovė (I2 = I3 = 0,33 A), nors viena varža už kitą didesnė net du kartus.
Klausimai ir užduotys
- Ką vadiname mišriuoju laidininkų jungimu?
- Tarkime, kad turite keturias elektros lemputes ir srovės šaltinį. Nubraižykite elektrines schemas, kai:
- lemputės sujungtos nuosekliai;
- lemputės sujungtos lygiagrečiai;
- lemputės sujungtos mišriai.
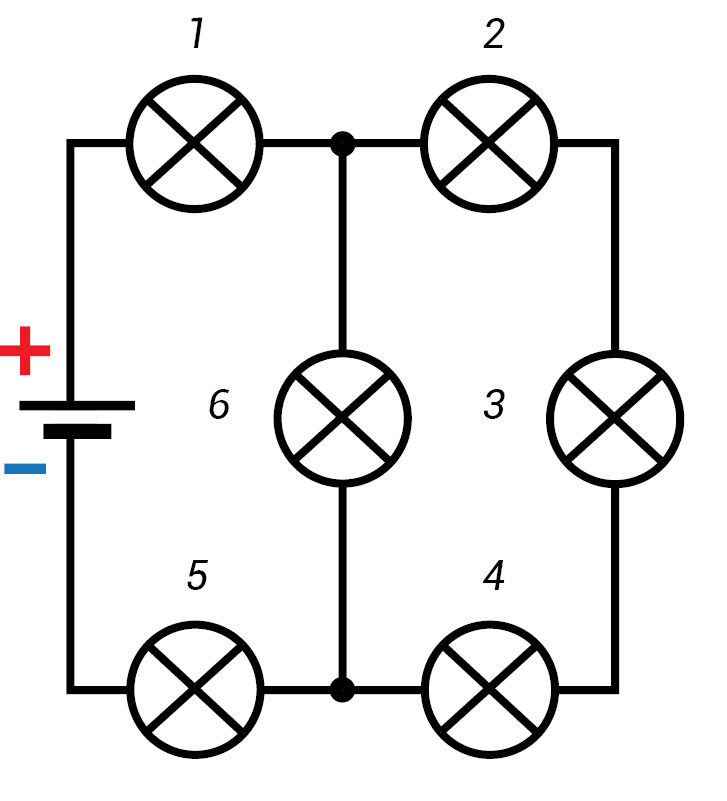
- 3.3.5 paveiksle pavaizduotoje elektrinėje schemoje yra šešios lemputės. Kokius lempučių jungimo būdus įžvelgiate? Apibūdinkite juos. Sąsiuvinyje nubraižykite supaprastintą elektrinę schemą ir joje pažymėkite elektros srovės kryptį.
- Remdamiesi mišriojo laidininkų jungimo nagrinėjimo pavyzdžiu (3.3.2 pav.) apskaičiuokite elektrinę įtampą kiekvieno varžo gnybtuose. (U1 = U4 = U5 = U6 = 5 V; U2 = 1,65 V; U3 = 3,3 V)
Mokomės spręsti uždavinius
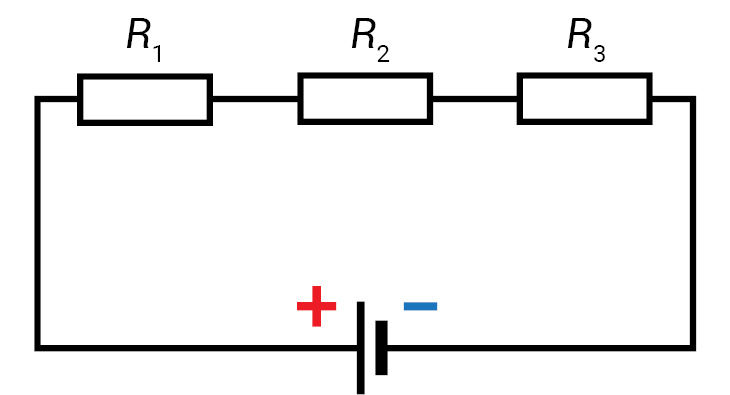
- Elektros grandinę sudaro trys nuosekliai sujungti (3.3.6 pav.) reostatai. Pirmo reostato varža 36 Ω, o gnybtų įtampa 18 V. Antro reostato varža 32 Ω. Elektrinė įtampa trečio reostato gnybtuose 120 V. Apskaičiuokite:
- antro reostato įtampą;
- trečio reostato varžą.
Sprendimas
- Per pirmą reostatą tekančios elektros srovės stipris:
Per antrą reostatą tekančios elektros srovės stipris:
Kadangi reostatai sujungti nuosekliai, tai
Kadangi (1 ir 2) lygčių kairės pusės yra lygios, turi būti lygios ir dešinės pusės:
Iš čia išreiškiame įtampą U2:
Į gautą lygtį įrašome skaitines dydžių vertes ir apskaičiuojame:
- Kadangi jungimas nuoseklusis, per pirmą ir trečią reostatus teka tokio pat stiprio elektros srovė:
Iš čia išreiškiame varžą R3:
Į gautą lygtį įrašome skaitines dydžių vertes ir apskaičiuojame:
Atsakymas: 16 V; 240 Ω.
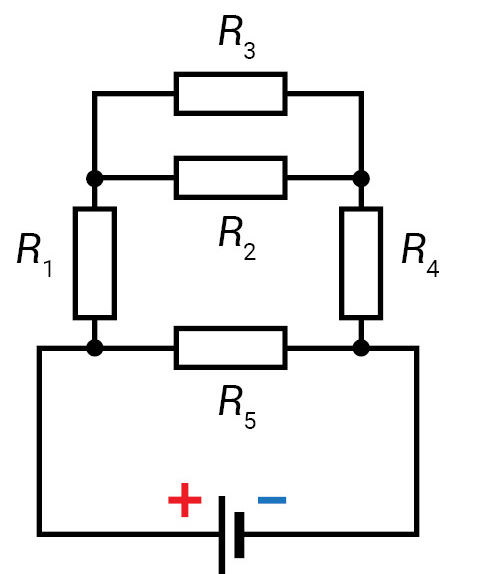
- 3.3.7 paveikslo (a) dalyje pavaizduotas mišrusis laidininkų jungimas, kai: R1 = 2 Ω, R2 = R3 = 10 Ω, R4 = 3 Ω, R5 = 40 Ω. Apskaičiuokite pilnutinę šios grandinės varžą.
Sprendimas
Iš elektros grandinės schemos matyti, kad varžai R2 ir R3 sujungti lygiagrečiai.
Varžų varžos yra vienodo didumo:
Pirminę elektros grandinės schemą (3.3.7 pav., a) pakeičiame antrine (3.3.7 pav., b). Iš jos matyti, kad varžas R1, varžų grupė R23 ir varžas R4 tarpusavyje sujungti nuosekliai:
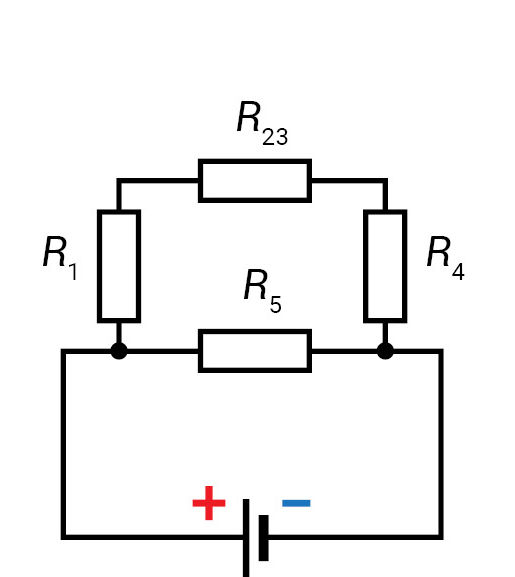
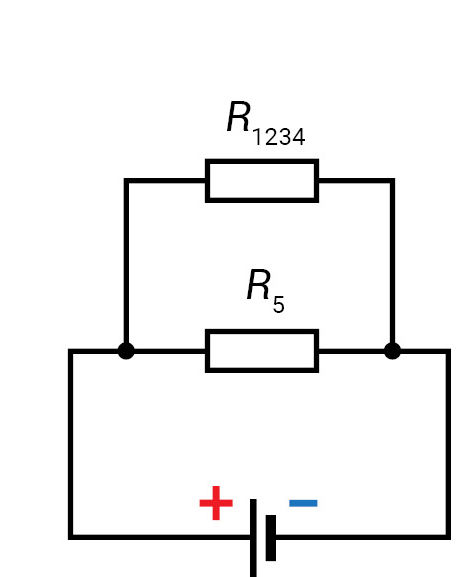
Antrinę elektros grandinės schemą (3.3.7 pav., b) pakeičiame trečia (3.3.7 pav., c). Varžų grupė R1234 ir penktas varžas tarpusavyje sujungti lygiagrečiai:
Atsakymas: 8 Ω.
Mokomės savarankiškai spręsti uždavinius
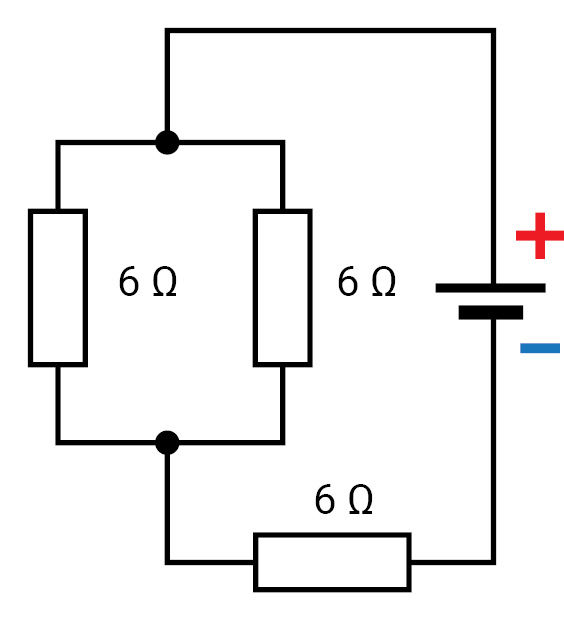
- 3.3.8 paveiksle pavaizduota elektros grandinės schema. Kiekvieno varžo varža lygi 6 Ω. Apskaičiuokite pilnutinę elektros grandinės varžą. (9 Ω)
- Varžai R1 ir R2 sujungti lygiagrečiai. Pirmu 55 Ω varžos varžu teka 4 A srovė, antru – 0,8 A. Nubraižykite elektrinę schemą. Apskaičiuokite antro varžo varžą. (275 Ω)
- Atlikdamas fizikos laboratorinį darbą Benas turėjo keturis 60 Ω varžos varžus. Berniukas iš jų sujungė šešias elektros grandines ir apskaičiavo pilnutines grandinių varžas: 15 Ω, 45 Ω, 60 Ω, 80 Ω, 150 Ω ir 240 Ω. Nubraižykite varžų jungimo schemas.
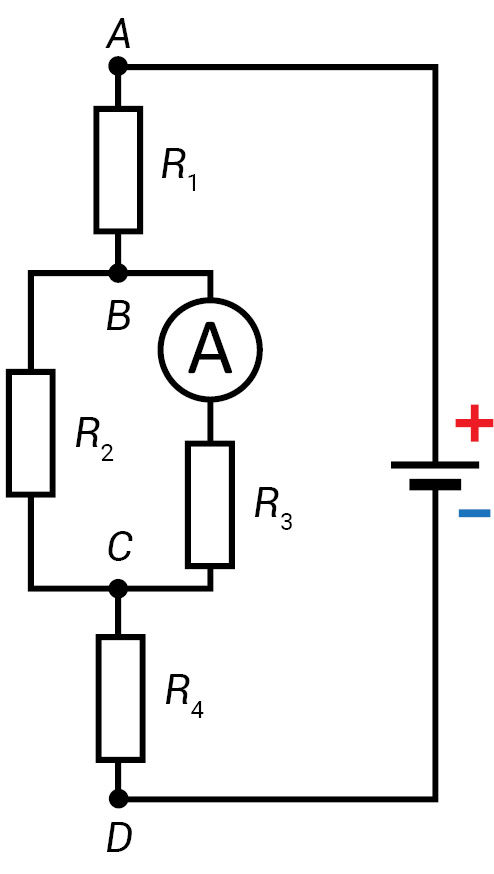
- 3.3.9 paveiksle pavaizduota mišriosios elektros grandinės schema. Laidininkų varžos yra tokios: R1 = 4 Ω, R2 = 6 Ω, R3 = 12 Ω, R4 = 2 Ω. Ampermetras rodo 1 A stiprio elektros srovę. Apskaičiuokite:
- elektrinę įtampą tarp taškų B ir C; (12 V)
- elektros srovės stiprį kiekviename laidininke; (I1 = 3 A; I2 = 2 A; I4 = 3 A)
- elektrinę įtampą pirmo ir ketvirto laidininkų gnybtuose; (UAB = 12 V; UDC = 6 V)
- srovės šaltinio įtampą. (30 V)
- Trys elektros srovės imtuvai, kurių varžos 20 Ω, 40 Ω ir 24 Ω, sujungti lygiagrečiai. Įtampa lygiagrečiai sujungtų imtuvų gnybtuose – 24 V. Remdamiesi šiais duomenimis, apskaičiuokite:
- elektros srovės stiprį kiekviename imtuve; (1,2 A; 0,6 A; 1 A)
- elektros srovės stiprį grandinėje; (2,8 A)
- pilnutinę grandinės varžą. (8,6 Ω)

