(Astronomija 11–12)

Elektromagnetinė spinduliuotė

SĄVOKOS:

energijos kvántas, fotònas, elektromagnètinės spinduliuõtės spèktras, šiluminė spinduliuõtė, juodàsis kūnas(visiškasis spinduõlis), šviẽsis

More like this

Elektromagnetinė spinduliuotė

Diduma žinių apie Visatos objektus ir joje vykstančius reiškinius gaunama iš elektromagnètinės spinduliuõtės (arba elektromagnètinių bangų), kurią šie objektai skleidžia arba atspindi. Kiekvieno objekto spinduliuotėje yra užkoduota informacija apie jo temperatūrą, sudėtį, greitį ir netgi terpės, per kurią ši spinduliuotė perėjo pakeliui į Žemę, savybes. Elektromagnetinė spinduliuotė yra ne tik informacijos apie astronominius objektus šaltinis, bet ir vienas iš pagrindinių energijos pernašos būdų Visatoje. Todėl svarbu susipažinti su jos ypatumais ir tyrinėjimo būdais.

More like this

Elektromagnetinių bangų skalė

Elektromagnetinės bangos apibūdinamos dažniu (ν) ir bangos ilgiu (λ). Šiuos dydžius sieja tokia priklausomybė:

v=\frac{c}{\lambda} (3.1.1)čia c – elektromagnetinės bangos sklidimo greitis.Visų elektromagnetinių bangų sklidimo greitis vakuume vienodas ir lygus c = 299 792 458 m ⁄ s ≅ 3 ∙ 108 m ⁄ s ir nepriklauso nuo jas skleidžiančio šaltinio judėjimo greičio. Tačiau elektromagnetinė spinduliuotė turi ne tik bangos, bet ir dalelių savybių. Ji sklinda ne tolydžiai, o tam tikromis porcijomis – energijos kvántais, arba fotònais, kurių energija proporcinga spinduliuotės dažniui arba atvirkščiai proporcinga jos bangos ilgiui. Proporcingumo koeficientas yra Planko konstanta:h=6,626\cdot10^{-34}\mathrm{\ J\cdot s}.Taigi, fotono energija lygi\mathrm{\varepsilon}=h\mathrm{\nu}=h\frac{c}{\lambda}. (3.1.2)Fotono energija yra labai mažas dydis, todėl ji paprastai matuojama ne įprastiniais SI sistemos energijos vienetais džáuliais (J), o elektronvòltais (eV):1\mathrm{eV}=1,60218\cdot10^{-19}\mathrm{J}.

Elektromagnetinių bangų ilgių intervalas labai platus: nuo 10^–3 m iki 10⁴ m. Trumpiausios bangos matuojamos pikometrais (1 pm = 10^–12 m) arba nanometrais (1 nm = 10^–9 m), ilgesnės bangos – mikrometrais (1 μm = 10^–6 m) arba milimetrais (mm), o ilgiausios – centimetrais (cm) ir metrais (m). Skirtingo ilgio elektromagnetinės bangos skirtingai sąveikauja su medžiagomis. Todėl ir jų spinduliuotės tyrimo metodai yra skirtingi. Atsižvelgiant į tai, elektromagnetinės bangos skirstomos į šešis diapazonus: gãma spindulių, reñtgeno spindulių, ultraviolètinių spindulių, regimõsios šviesos, infraraudonųjų spindulių ir rãdijo bangų diapazonus (3.1.1 lentelė). Infraraudonųjų spindulių spektro ruožas nuo 0,3 mm iki 1 mm dažnai vadinamas submilimetriniù diapazonù, o radijo bangų ilgių intervalas nuo 1 mm iki 0,3 m – mikrobangų diapazonù.

3.1.1 lentelė. Elektromagnetinės spinduliuotės spektro diapazonai

Diapazonas	Bangos ilgių intervalas, Δλ	Žemės atmosferos skaidrumas
Gama spinduliai	<10 pm	Neskaidri; spinduliuotę sugeria oro atomai ir molekulės (azotas, deguonis ir kt.)
Rentgeno spinduliai	10 pm–10 nm	Taip pat
Ultravioletiniai spinduliai	10–400 nm	Iki 320 nm – taip pat; nuo 320 nm – iš dalies skaidri
Regimoji šviesa	400–700 nm	Beveik skaidri
Infraraudonieji spinduliai	700 nm–1 mm	Iš dalies skaidri atskiruose bangų ilgių ruožuose; kitur neskaidri (vandens, anglies dioksido ir kt. molekulių sugertis)
Radijo bangos	>1 mm	Skaidri atskiruose bangų ilgių ruožuose

Fotono energija

Uždavinys. Žalios šviesos bangos ilgis λ = 510 nm. Kokia šio bangos ilgio fotono energija?SprendimasŠviesos bangos ilgis \lambda=510\mathrm{\ nm}=0,51\cdot10^{-6}\mathrm{\ m.}Šviesos greitis c=3\cdot10^{8\ }\mathrm{m\cdot s^{-1}}Planko konstanta h=6,626\cdot10^{-34}\mathrm{J\cdot s}.Fotono energija \mathrm{\varepsilon}=h\frac{c}{\lambda}=6,626\cdot10^{-3}\cdot\frac{3\cdot10^8}{0,51\cdot10}\approx

3,898\cdot10^{-19}\mathrm{\left(J\right)=2,}43\left(\mathrm{eV}\right).

Žmogaus akys mato regimąją šviesą ir joje skiria septynias pagrindines spalvas: violetinę (400–450 nm), mėlyną (450–485 nm), žydrą (485–500 nm), žalią (500–565 nm), geltoną (565–590 nm), oranžinę (590–625 nm) ir raudoną (625–700 nm).

Spinduliuotė, pasiekianti mus iš Visatos tolių, apima visus elektromagnetinio spektro diapazonus. Tačiau kiekviename diapazone savo šviesumu išsiskiria vis kiti objektai. Pavyzdžiui, gama ir rentgeno spindulių diapazone šviesiausios yra tolimos aktyviosios galaktikos ir karštos tarpgalaktinės dujos galaktikų spiečiuose, o ultravioletinių spindulių ruože – masyvios ir karštos žvaigždės. Regimosios šviesos diapazone matome artimesnius Saulės sistemos kūnus, žvaigždes ir galaktikas. Infraraudonųjų spindulių diapazone šviesiausios yra žemų temperatūrų žvaigždės, tarpžvaigždinės medžiagos debesys. Radijo bangose savo spinduliuote išsiskiria vadinamosios radiogalaktikos ir šalti tarpžvaigždinių dujų debesys. Taigi, astronominiai objektai ir visas dangus skirtinguose spektro ruožuose atrodytų vis kitokie.

Per Žemės atmosferą pereina ne visų bangų ilgių elektromagnetinė spinduliuotė, atsklindanti iš astronominių objektų. Nemažą jos dalį sugeria ir išsklaido Žemės atmosferos atomai ir molekulės (žr. 3.1.1 lentelę ir 3.1.1 pav.).

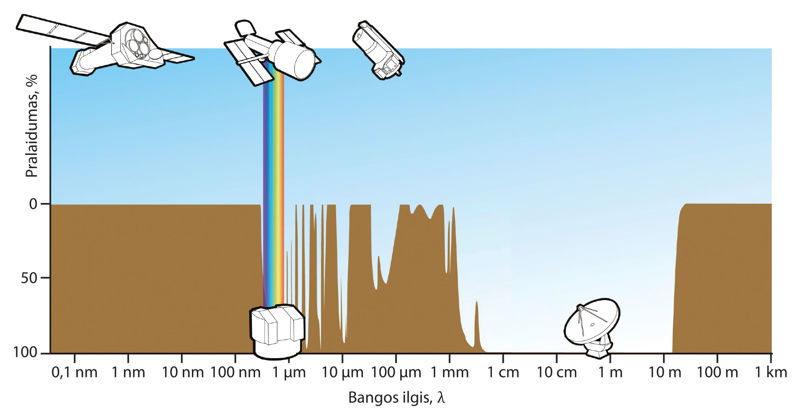
3.1.1 pav. Žemės atmosferos pralaidumas elektromagnetinei spinduliuotei. Nuo Žemės paviršiaus galimi tyrimai tik regimosios šviesos ir radijo bangų ruožuose. Visus elektromagnetinių bangų diapazonus galima tyrinėti su kosminiais teleskopais.

Svarbiausias yra vadinamasis òptinis lángas, apimantis elektromagnetinio spektro ruožą nuo 320 nm iki 1 μm. Taip yra dėl kelių priežasčių. Šiame lange yra ir regimosios šviesos diapazonas, kuriame matome tiriamus astronominius objektus. Be to, astronominius stebėjimus pro optinį langą galima atlikti su teleskopais, esančiais ant Žemės. Kitas spektro ruožas, kuriame stebėjimus įmanoma atlikti su Žemėje įrengtais radioteleskòpais, yra radijo bangų ruožas nuo 1 mm iki 20 m. Astronominių objektų spinduliuotė kituose spektro ruožuose tyrinėjama su kosminiais teleskopais.

Klausimai ir užduotys

Palyginkite rentgeno ir infraraudonųjų spindulių fotonų energiją. Kurio iš šių fotonų energija didesnė?
Kokie yra elektromagnetinės spinduliuotės diapazonai?
Kodėl astronomai negali tyrinėti dangaus kūnų visuose elektromagnetinio spektro diapazonuose iš antžeminių observatorijų?
Kosminis teleskopas gali registruoti fotonus, kurių energija siekia 100 keV (kiloelektronvòltų). Koks tokių fotonų elektromagnetinės bangos ilgis? Kokiame spektro diapazone spinduliuojami šie fotonai?

More like this

Šiluminės spinduliuotės dėsningumai

Visi Žemėje ar Visatoje esantys kūnai, kurių temperatūra aukštesnė už absoliutųjį nulį (0 K = –273,15 °C) skleidžia elektromagnetinę spinduliuotę beveik visais bangos ilgiais. Gamtoje labiausiai paplitusi šiluminė, arba temperatūrinė, spinduliuõtė, kurią sukelia medžiagos dalelių šiluminiai virpesiai. Žemos temperatūros aplinkoje kūnas skleidžia tik infraraudonuosius spindulius ir radijo bangas. Aukštos temperatūros aplinkoje kūnas skleidžia regimąją šviesą ir ultravioletinius spindulius. Kuo aukštesnė temperatūra, tuo platesnis spinduliuojamų dažnių diapazonas. Be to, kylant temperatūrai, didėja bet kurio dažnio spinduliuotės galia.

Šiluminės spinduliuotės dėsningumai apibūdinami remiantis júodojo kūno (visiškojo spinduõlio) modeliu. Pagrindinė juodojo kūno savybė yra ta, kad jis, nesvarbu, kokia jo temperatūra, sugeria visą įvairių bangos ilgių elektromagnetinę spinduliuotę, krintančią į jo paviršių. Júodojo kūno sugerties gebà (sugertos ir į jo paviršių kritusios spinduliuotės energijos santykis) lygi 1. Júodojo kūno spinduliuõtės gebà, t. y. iš jo paviršiaus vienetinio ploto visomis kryptimis išspinduliuojamos energijos kiekis per laiko vienetą, priklauso tik nuo jo temperatūros, bet nepriklauso nuo medžiagos ir formos. Realybėje nėra objektų, kurių šiluminė spinduliuotė tiksliai atitiktų juodojo kūno spinduliuotę. Tačiau daugelio astronominių objektų (žvaigždžių, tarpžvaigždinių ūkų, planetų ir jų palydovų) šiluminę spinduliuotę galima apytiksliai prilyginti juodojo kūno spinduliuotei ir tuo remiantis įvertinti jų temperatūras bei kitus fizinius parametrus. 3.1.2 pav. pavaizduotas juodojo kūno spinduliuotės gebos ε(λ), išreikštos santykiniais vienetais, spektrinis skirstinys įvairios temperatūros aplinkose.

3.1.2 pav. Juodojo kūno spinduliuotės energijos skirstinys įvairios temperatūros aplinkose

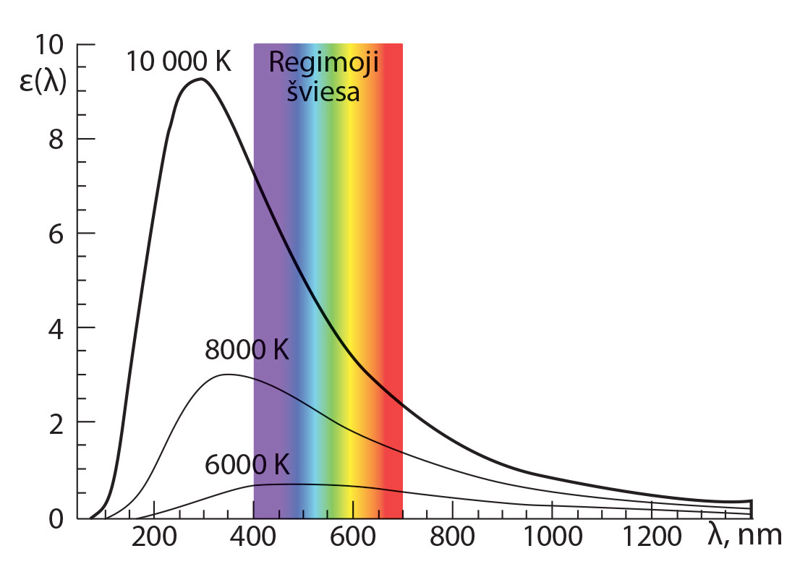
Iš šios iliustracijos galime padaryti tokias išvadas:

Juodojo kūno spinduliuotės spektras yra ištisinis, t. y. visame bangos ilgių diapazone spinduliuoja mos visų galimų bangos ilgių (dažnių) bangos.
Karštesnio kūno kreivė yra aukščiau vėsesnio kūno kreivės visame bangų ilgių diapazone. Tai rodo, kad kiekvieno bangos ilgio ruože karštesni kūnai spinduliuoja daugiau energijos iš vienetinio ploto.
Kiekviena kreivė turi bangos ilgį \lambda_{\mathrm{\max}}, kuriame spinduliuotės geba pasiekia maksimumą. Kuo aukštesnė kūno temperatūra, tuo didesnis λ_max poslinkis į trumpųjų bangų pusę.

Vokiečių fizikas Vilhelmas Vynas (Wilhelm Wien, 1864–1928) nustatė tokį λ_max ir juodojo kūno absoliučiosios temperatūros sąryšį:\lambda\mathrm{_{\max}}=\frac{b}{T} (3.1.3)čia b – Vyno poslinkio dėsnio konstanta.(3.1.3) sąryšis vadinamas Výno póslinkio dėsniu.Susumavę juodojo kūno spinduliuotės gebas ε_λ,Tper visus bangos ilgius gausime visuminę spinduliuotės gebą ε_T, kurią astronomai paprastai vadina júodojo kūno spinduliuõtės galià kūno plóto vienetui. Austrų fizikai Jozefas Štefanas (Josef Stefan) ir Liudvigas Eduardas Bolcmanas (Ludwig Eduard Boltzmann) nustatė ε_T ir juodojo kūno absoliučiosios temperatūros sąryšį. Tas sąryšis dabar vadinamas Štèfano ir Bòlcmano dėsniu, teigiančiu, kad juodojo kūno spinduliuotės galia proporcinga kūno absoliučiajai temperatūrai ketvirtuoju laipsniu:

ε_{T} = σ T^{4}

; (3.1.4)

čia σ – Štefano ir Bolcmano konstanta.

Pagal šį dėsnį apskaičiuotos galios dimensija:

\left[\mathrm{\varepsilon}_T\right]=\mathrm{W}\cdot\mathrm{m^{-2}}.Jei žinome šviesulio temperatūrą ir paviršiaus plotą, tai remdamiesi Štefano ir Bolcmano dėsniu galime apskaičiuoti jo skleidžiamos spinduliuotės galią. Pavyzdžiui, žvaigždės paprastai laikomos karštų dujų (plazmos) kamuoliais (rutuliais). Jei žvaigždės paviršiaus (fotosferos) temperatūra T ir spindulys R, tai jos spinduliuotės galia, astronomų vadinama šviesiù, bus lygi $L = 4 π R^{2} σ T^{4}$ . (3.1.5)

Šviẽsio dimeñsija: [L] = W.

Planko formulė

Juodojo kūno spinduliuotės gebos analizinę išraišką išvedė vokiečių fizikas Maksas Plankas (Max Planck, 1858–1947). Jei ši geba išreikšta kaip bangos ilgio funkcija, tai formulė tokia:

\mathrm{\varepsilon}_{\lambda,\ T}=\frac{2\pi hc^2}{\lambda^5}\left(e^{\frac{hc}{\lambda kT}}-1\right)^{-1}.Jei ši geba išreikšta kaip dažnio funkcija, tai formulė tokia:\mathrm{\varepsilon}_{v,\ T}=\frac{2\pi hc^3}{c^2}\left(e^{\frac{hv}{kT}}-1\right)^{-1}.čia h – Planko konstanta, c – šviesos greitis, k – Bolcmano konstanta, T – kūno absoliučioji temperatūra, λ – bangos ilgis, \nu – dažnis.Remiantis spinduliuotės gebos apibrėžimu, jos dimensija SI sistemoje yra tokia:\left[\mathrm{\varepsilon}_{\lambda,\ T}\right]=\mathrm{W\cdot m^{-2}nm^{-1}}, jei geba išreikšta kaip bangos ilgio funkcija;\left[\mathrm{\varepsilon}_{\nu,\ T}\right]=\mathrm{W\cdot m^{-2}Hz^{-1}}, jei geba išreikšta kaip dažnio funkcija.3.1.2 pav. pateiktos kreivės apskaičiuotos taikant Planko formulę.Kai nagrinėjami bangų ilgiai yra daug didesni už λ_max (λ ≫ λ_max), Planko funkciją galima aproksimuoti paprastesne išraiška, vadinama Reilio (Rayleigh) ir Džinso (Jeans) artiniu (dėsniu):\mathrm{\varepsilon}_{\lambda,\ T}=\frac{2\pi ckT}{\lambda^4}Šis artinys dažnai taikomas radioastronomijoje.

Juodojo kūno spinduliuotės dėsnių taikymas

1 uždavinys. Žmogaus kūno temperatūra apie 310 K. Koks bangos ilgis, kuriame žmogaus kūnas skleidžia daugiausia energijos?SprendimasTaikysime Vyno poslinkio dėsnį (3.1.3 formulę).Žmogaus kūno temperatūra T = 310 K.Vyno poslinkio dėsnio konstanta b = 2,9 ∙ 10^–3 m ∙ K.Bangos ilgis\lambda_{\max}=\frac{b}{T}=\frac{2,9\cdot10^{-3}}{310}\approx

9,4\cdot10^{-6}\left(\mathrm{m}\right)=9,4\left(\mathrm{\mu m}\right)

2 uždavinys. Saulė daugiausia energijos išspinduliuoja 500 nm ilgio bangomis. Kokia Saulės paviršiaus (fotosferos) temperatūra?SprendimasTaikysime Vyno poslinkio dėsnį (3.1.3 formulę).Bangos ilgis λ_max = 500 nm = 5 ∙ 10^–7 m.Saulės paviršiaus (fotosferos) temperatūra

T_{⊙} = \frac{b}{λ_{\max}} =

\frac{2,9\cdot10^{-3}}{5\cdot10^{-7}}=

5800 (K)

3 uždavinys. Apskaičiuokite Saulės šviesį (spinduliuotės galią), jei jos fotosferos temperatūra T_⊙ = 5800 K (kaip apskaičiuota 2 uždavinyje), o spindulys R_⊙= 6,957 ∙ 10⁸ m.

Sprendimas

Taikysime Štefano ir Bolcmano dėsnį (3.1.4 formulę).

Saulės šviesis

L_⊙ = 4πR²_⊙ σT_⊙⁴ =
= 4π(6,957 ∙ 10⁸)² ∙ 5,67 ∙ 10^–8 ∙ 5800⁴ = 3,90 ∙ 10²⁶ (W).

Klausimai ir užduotys

Koks kūnas vadinamas juoduoju kūnu?
Belatriksės (γ Ori, Oriono γ) atmosferos temperatūra 21 800 K. Kokio ilgio bangomis Belatriksė išspinduliuoja daugiausia energijos? Kuriame spektro diapazone yra šis bangos ilgis?
Pelė yra vienas iš aktyviausių Jupiterio palydovo Ijo ugnikalnių. Jame tyvuliuojanti lava yra įkaitusi iki 1500 K, o vidutinė Ijo paviršiaus temperatūra siekia tik apie 110 K. Apskaičiuokite, kiek kartų spinduliuotės galia, sklindanti iš Pelės ugnikalnio 1 m² lavos ploto, yra didesnė už spinduliuotės galią, kurią spinduliuoja 1 m² Ijo paviršiaus plotas, esantis už ugnikalnio ribų.
Panagrinėkite elektromagnetinės spinduliuotės spektrą ir juodojo kūno spinduliuotės dėsningumus pasitelkę pateikiamas programėles.