Tema 2.9 (Astronomija 11–12)

Regimasis planetų judėjimas

SĄVOKOS:

planetà, planètų konfigūrãcijos: elongãcija, jungtis, opozicija, kvadratūrà; geocentrinis mòdelis, heliocentrinis mòdelis, sinòdinis periòdas, žvaigždinis arbà orbitinis periòdas

Daugiau
Daugiau pasirinkimų

Regimasis planetų judėjimas

Dar senovės astronomai pastebėjo, kad, be Saulės ir Mėnulio, Zodiako žvaigždynais netoli ekliptikos juda penki į žvaigždes panašūs šviesuliai. Senovės graikai tuos šviesulius pavadino „klajojančiomis žvaigždėmis“ – planètomis1. Jos buvo pavadintos dievų vardais: Merkùrijus, Venerà, Mársas, Jupiteris ir Satùrnas. (Kitos dvi planetos Urãnas ir Neptūnas atrastos vėliau, XVIII–XIX a.)

1 Planetà [gr. πλάνητες ἀστέρες (plànētes astéres) – klajojančios žvaigždės]

Planetų regimasis judėjimas iš pirmo žvilgsnio atrodo itin sudėtingas ir tarytum pateisina klajoklių pavadinimą. Tam tikrą laiko dalį planeta, kaip Saulė ir Mėnulis, slenka Zodiako žvaigždynais iš vakarų į rytus. Tai vadinama planetos tiesióginiu judėjimu. Praėjus tam tikram laiko tarpui ji stabteli ir toliau ima slinkti į priešingą pusę, t. y. vakarų kryptimi. Tai vadinama planetos atgaliniù judėjimu. Atgalinis judėjimas baigiasi trumpu stabtelėjimu, o toliau planeta vėl pereina į tiesioginį judėjimą, ir vėl jos judėjimo ciklas kartojasi. Kai planetos regimasis judėjimas pereina nuo tiesioginio prie atgalinio ir vėl grįžta prie tiesioginio judėjimo, jos regimojo judėjimo takas piešia kilpas arba zigzagus nejudančių žvaigždžių rašto fone. Regimoji planetos padėtis Saulės atžvilgiu apibūdinama elongãcija2– kampiniu atstumu nuo Saulės (kampu tarp krypčių „stebėtojas-planeta“ ir „stebėtojas-Saulė“). Jei planeta matoma į rytus nuo krypties į Saulę, tai ji yra rytų elongãcijoje, jei į vakarus  – vakarų elongãcijoje.

2 Elongãcija [lot. elongatio – nutolimas]

Greičiausiai Zodiako žvaigždynais judančios planetos – Merkurijus ir Venera, dar vadinamos vidinėmis planètomis, tarytum švytuoja apie Saulę pernelyg nuo jos nenutoldamos. Merkurijaus didžiausia elongacija siekia 28°, o Veneros – 48°. Kai šios planetos būna rytų elongacijoje, jos matomos vakarais tuoj po saulėlydžio. Venera tada vadinama Vakarinè (žvaigžde). Kai šios planetos būna vakarų elongacijoje, jos matomos rytais prieš saulėtekį. Venera tuomet vadinama Rytinè (žvaigžde). Kai planeta, slinkdama rytų kryptimi (tiesioginis judėjimas) nuo didžiausios vakarų elongacijos priartėja prie Saulės ir galiausiai pasislepia Saulės spinduliuose, tada ji būna viršutinėje jungtyjè su Saule, o jos elongacija lygi 0°. Kai planeta, slinkdama vakarų kryptimi (atgalinis judėjimas) nuo didžiausios rytų elongacijos priartėja prie Saulės ir galiausiai pasislepia Saulės spinduliuose, tada ji būna apatinėje jungtyjè su Saule, o jos elongacija lygi 0°.

Kitaip žvaigždžių atžvilgiu juda likusios, vadinamosios išorinės planètos: Marsas, Jupiteris ir Saturnas (taip pat Uranas ir Neptūnas). Jų regimasis judėjimas yra lėtesnis negu vidinių planetų ir Saulės. Bet jos gali būti matomos įvairiose elongacijose. Didesnę laiko dalį jų judėjimas yra tiesióginis, t. y. iš vakarų į rytus. Kai planeta matoma vakaruose tuoj po saulėlydžio (rytų elongacijoje), ji, kaip ir Saulė, slenka į rytus žvaigždžių atžvilgiu (tiesioginis judėjimas). Tačiau juda lėčiau nei Saulė, todėl po tam tikro laiko slepiasi Saulės spinduliuose ir leidžiasi kartu su Saule. Tada ji yra jungtyjè su Saule, o jos elongacija lygi 0°. Vėliau, kai Saulė gerokai aplenkia planetą, ji tampa matoma vakarų elongacijoje rytais prieš saulėtekį. Kai planeta atslenka į žvaigždynus, esančius priešingoje nuo Saulės dangaus pusėje, jos tiesioginis judėjimas sulėtėja. Trumpai stabtelėjusi ji ima judėti vakarų kryptimi (atgalinis judėjimas). Praėjus nedideliam laiko tarpui planeta vėl stabteli ir ima judėti rytų kryptimi (tiesioginis judėjimas) tol, kol ją vėl paveja Saulė. Atgalinio judėjimo atkarpos viduryje planetos elongacija lygi 180°, ir ji matoma Zodiako žvaigždyne, kuris yra priešingoje nuo Saulės pusėje. Ši planetos padėtis vadinama opozicija Saulės atžvilgiu. Kitos svarbios išorinių planetų regimosios padėtys Saulės atžvilgiu yra rytų kvadratūrà, jei jos rytų elongacija lygi 90°, ir vakarų kvadratūrà, jei jos vakarų elongacija lygi 90°. Planetos tiesioginio ir atgalinio judėjimo iliustracijoje (žr. 2.9.1 pav.) pavaizduotas Marso regimasis judėjimas Tauro žvaigždynu.

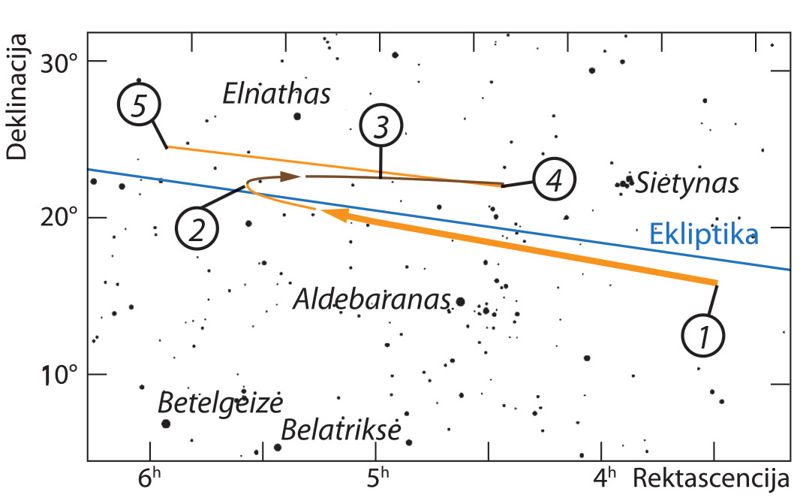
2.9.1 pav. Regimasis Marso judėjimo takas per Tauro žvaigždyną 2022 m. rugpjūčio mėn. – 2023 m. kovo mėn. laikotarpiu. Tako atkarpos: 1–2 ir 3–4 – tiesioginis judėjimas, 2–4 – atgalinis judėjimas, 3 – opozicija.

Šios apibūdintos regimosios vidinių ir išorinių planetų padėtys Saulės atžvilgiu vadinamos planetos konfigūrãcijomis.

Laiko tarpas tarp gretimų vienas po kito įvykstančių planetos perėjimų per tą pačią konfigūraciją vadinamas planetos sinòdiniu3 periodù.

3 Sinòdinis [gr. συνοδικός (synodikós) – jungtis, susitikimas]

Tai gali būti, pavyzdžiui, laiko tarpas tarp gretimų opozicijų arba tarp gretimų jungčių.

Dar senovės Graikijos mokslininkai, bandydami paaiškinti pasaulio (Saulės sistemos) sandarą, nagrinėjo du modelius: geocentrinį ir heliocentrinį. Geocentriniame modelyje pasaulio centru buvo Žemė, aplink kurią sukasi Mėnulis, Saulė, planetos ir žvaigždės. Heliocentriniame modelyje pasaulio centru buvo Saulė, aplink kurią sukasi visi kiti dangaus kūnai, taip pat ir Žemė. Heliocentrinis modelis nesulaukė plataus senovės astronomų palaikymo, nes tuo metu įrodymų, kad Žemė juda orbita aplink Saulę, nebuvo. Dauguma astronomų rėmėsi regimuoju įvaizdžiu, kad Žemė yra nejudantis pasaulio centras, aplink kurį sukasi visi dangaus šviesuliai. Remdamasis ankstesnių astronomų darbais, II a. gyvenęs graikų mokslininkas Klaudijas Ptolemajas sukūrė matematinį geocentrinės pasáulio sistèmos mòdelį. Planetų regimasis tiesioginis ir atgalinis judėjimas buvo aiškinamas gana sudėtingai. Bet kurios planetos regimojo judėjimo trajektorija buvo planetos judėjimų keliais apskritimais derinys, matomas iš Žemės perspektyvos (plačiau apie Ptolemajo sistemą žr. skiltyje „Klaudijas Ptolemajas“).

Heliocentrinį pasáulio mòdelį išplėtojo ir aprašė 1543 m. lenkų astronomas Mikalojus Kopernikas veikale „Apie dangaus sferų sukimąsi“. Pagal šį modelį pasaulio (Saulės sistemos) centre yra Saulė. Visos planetos, tarp jų ir Žemė, tolygiais greičiais skrieja aplink Saulę apskritiminėmis orbitomis, kurių plokštumos maždaug sutampa. Aplink Žemę skrieja tik vienintelis jos palydovas Mėnulis (plačiau apie Koperniko sistemą skaitykite skiltyje „Mikalojus Kopernikas“). Netoli Saulės matomų Merkurijaus ir Veneros planetų orbitos yra Žemės orbitos viduje (todėl tai vidinės planetos). Kitų planetų orbitos yra Žemės orbitos išorėje (todėl tai išorinės planetos). Šį modelį toliau ištobulino vokiečių astronomas Johanesas Kepleris. Jis nustatė tris planetų judėjimo dėsnius.

Regimasis planetų judėjimas pagal Koperniko modelį paaiškinamas paprasčiau ir natūraliau nei Ptolemajo modelis. Kadangi planetas stebime iš orbita aplink Saulę judančios Žemės, tai regimasis jų judėjimas yra Žemės ir planetos orbitinių judėjimų atstojamasis judėjimas. Tiesioginį ir atgalinį planetos judėjimą (2.9.1 pav.) paaiškina 2.9.2 pav., kuriame pateikta Žemės ir Marso planetų judėjimo schema.

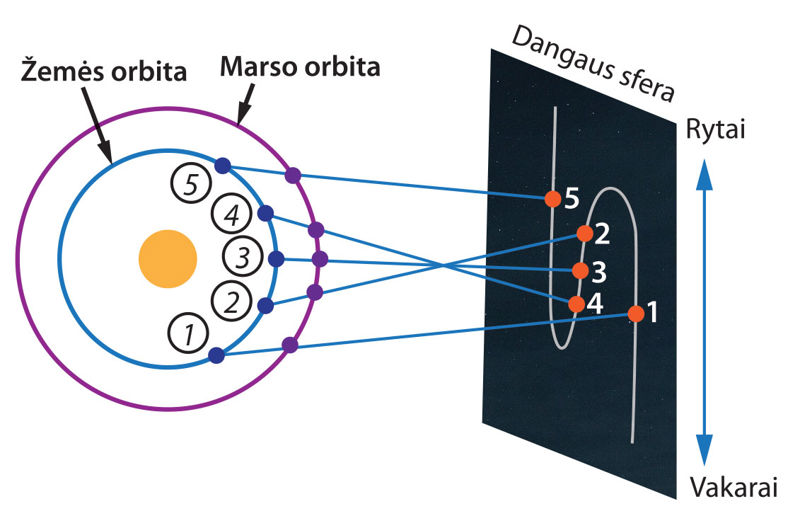
2.9.2 pav. Schema, paaiškinanti išorinės planetos Marso regimąjį tiesioginį ir atgalinį judėjimą. 2–3–4 – atgalinis judėjimas, 3 – opozicija.

Kadangi Žemė skrieja arčiau Saulės, jos orbitinis greitis yra didesnis už išorinės planetos Marso orbitinį greitį. Tam tikru momentu Žemė pasiveja Marsą ir aplenkia. Kaip tik tuo metu stebėtojas Žemėje mato, kad Marso regimasis tiesioginis judėjimas pasikeičia į atgalinį judėjimą.

Šio skyrelio pradžioje aptartas planetų konfigūracijas paprasta paaiškinti remiantis heliocentriniu modeliu, kaip parodyta 2.9.3 pav.

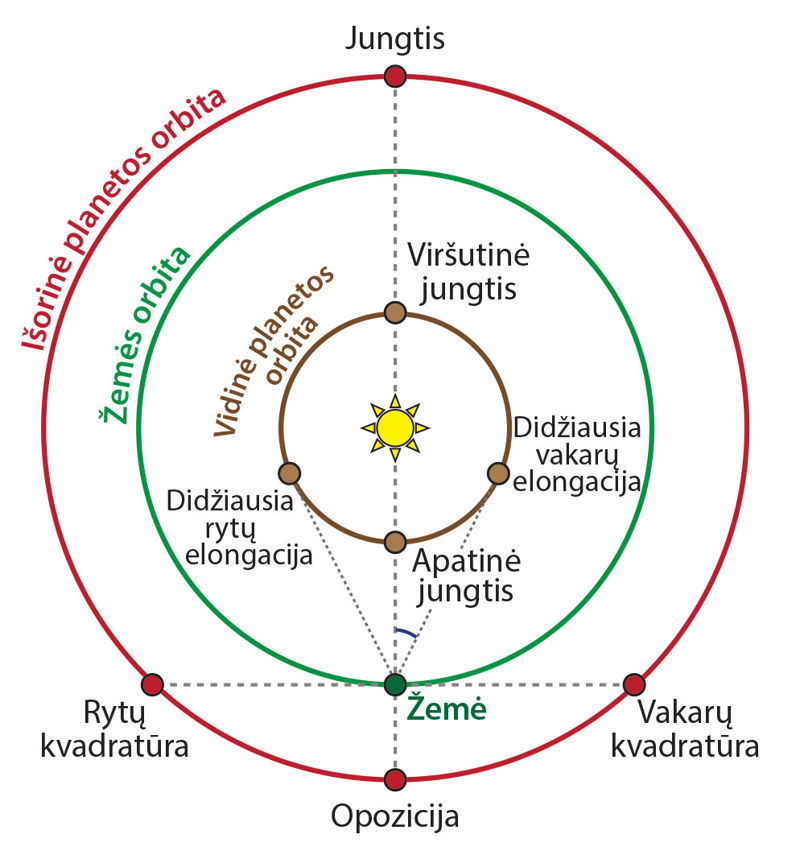
2.9.3 pav. Schema, paaiškinanti pagrindines planetų konfigūracijas

Jei vidinių planetų orbitų plokštumos sutaptų su ekliptikos plokštuma, tai per kiekvieną apatinę jungtį (kiekvieną sinodinį periodą) vidinė planeta praslinktų priešais Saulės diską, t. y. būtų stebimas planètos tranzitas. Tačiau Merkurijaus ir Veneros orbitos yra pasvirusios į ekliptiką nedideliu kampu. Todėl šių planetų tranzitai nėra tokie dažni. Dažniau įvyksta Merkurijaus tranzitai – kas 3–10 metų (2019, 2032, 2039, 2049, 2052, 2062 ir t. t.). O Veneros tranzitai gana reti – paskutinis įvyko 2012 m., bet kito, artimiausio, tranzito teks palaukti iki 2117 m.

Kaip jau buvo pažymėta, stebint planetos perėjimus per konfigūracijas galima nustatyti jos sinodinį periodą. Tačiau mums svarbesnis yra tikrasis planètos orbitinis periòdas, arba žvaigždinis periòdas.

Planètos orbitinis periòdas, arba žvaigždinis periòdas, yra laiko tarpas, per kurį planeta vieną kartą apskrieja Saulę nejudančių žvaigždžių atžvilgiu.

Tiesiogiai išmatuoti planetos orbitinio periodo (P) negalime. Tačiau šį periodą galime apskaičiuoti, jei žinome planetos sinodinį periodą (S) ir Žemės orbitinį (žvaigždinį) periodą (P⊕), dar vadinamą žvaigždiniais metais. Šiuos tris periodus sieja sinòdinio judėjimo lygtis.

Sinodinio judėjimo lygtis išorinei planetai:

1S=1P⊕-1P. (2.9.1)

Sinodinio judėjimo lygtis vidinei planetai:

1S=1P-1P⊕. (2.9.2)

Atliekant skaičiavimus pagal šias formules, visi periodai gali būti išreikšti ne tik saulinėmis paromis, bet ir kitais laiko vienetais (metais, valandomis ar sekundėmis). Atitinkamais vienetais bus gautas ir atsakymas.

Sinodinio judėjimo lygtis gali taikyti ir Žemėje, ir kitoje planetoje esantis stebėtojas. Pavyzdžiui, jei stebėtojas būtų Marse, tai galėtų apskaičiuoti Žemės sinodinį periodą, stebimą iš Marso. Žemė būtų vidinė planeta Marso atžvilgiu (taikytume (2.9.2) formulę). Tada planetos orbitiniu periodu P turėtų būti Žemės orbitinis periodas, o vietoj P⊕ turėtų būti Marso orbitinis periodas.

Sinodinio judėjimo lygtis

Pažymėkime: S – išorinės planetos sinodinį periodą, P – jos orbitinį (žvaigždinį) periodą, P⊕– Žemės orbitinį periodą (žvaigždinius metus). Tegul visi dydžiai bus išreikšti saulinėmis paromis. Tada per parą planeta pasislinks orbita kampu \frac{360\degree}{P}, o Žemė – \frac{360\degree}{P}. Regimasis planetos kampinis poslinkis, kurį matys Žemės stebėtojas, bus lygus \frac{360\degree}{S}, t. y. Žemės ir planetos kampinių poslinkių orbitoje skirtumui:

1S=1P-1P⊕.

Gavome sinodinio judėjimo lygtį išorinei planetai.

Analogiškai išvedama ir sinodinio judėjimo lygtis vidinei planetai.

Klaudijas Ptolemajas (100–170)

Klaudijas Ptolemajas (Κλαύδιος Πτολεμαiος, Klaudios Ptolemaios) gyveno ir dirbo Aleksándrijoje, Egiptè. Svarbiausias jo veikalas „Astronomijos sandara“, plačiau žinomas pavadinimu „Almagestas“, paskelbtas apie 150 m. Šiame veikale aprašytas geocentrinio pasaulio modelis, kurio schema pavaizduota 2.9.4 pav. Centre yra nejudanti Žemė. Šviesuliai orbitose išdėstyti atsižvelgiant į jų regimąjį judėjimo greitį dangaus sferoje: artimiausi juda greičiausiai, o tolimiausi – lėčiausiai. Toliau už Saturno orbitos yra nejudančių žvaigždžių sfera (neparodyta). Šviesulių tekėjimas ir laida aiškinami dangaus sferos sukimusi aplink Žemę iš rytų į vakarus. Be to, Saulė ir Mėnulis juda aplink Žemę iš vakarų į rytus didžiaisiais apskritimais (defereñtais) (tiesioginis judėjimas).

Planetos juda mažaisiais apskritimais (epiciklais), o jų centras – didžiuoju apskritimu. Planetų judėjimas epiciklais buvo sumanytas tam, kad būtų modeliuojamas atgalinis planetų judėjimas. Derinant didžiųjų ir mažųjų apskritimų parametrus ir planetų judėjimo greičius, buvo galima sumodeliuoti planetos regimąjį judėjimą dangaus sferoje, atitinkantį stebėjimų duomenis, ir apskaičiuoti Saulės, Mėnulio ir planetų padėtis daugeliui metų į priekį. Dėl to šis modelis planetų padėtims apskaičiuoti buvo taikomas beveik 15 amžių. Didėjant astronominių matavimų tikslumui, buvo pastebimi vis ryškesni išmatuotų ir apskaičiuotų pagal Ptolemajo modelį planetų padėčių skirtumai. Siekiant sumažinti šiuos skirtumus, viduramžiais Ptolemajo modelis buvo tobulinamas įvedant papildomus epiciklus. Dėl to ilgainiui modelis tapo itin sudėtingas ir nepatogus taikyti. Būtina pastebėti, kad Ptolemajas savo modelį laikė tik tinkamu matematiniu metodu dangaus šviesulių regimosioms padėtims apskaičiuoti, bet niekada neteigė, kad šviesuliai realybėje juda tokiomis sudėtingomis trajektorijomis.

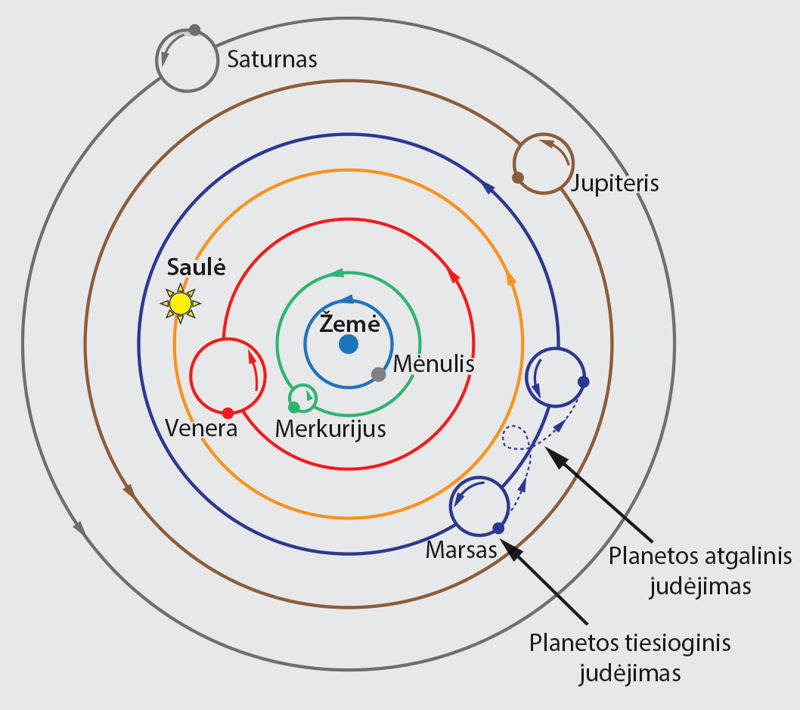
2.9.4 pav. Ptolemajo geocentrinės pasaulio sistemos modelis

Mikalojus Kopernikas (1473–1543)

Lenkų astronomas Mikalojus Kopernikas (lenk. Mikołaj Kopernik, lot. Nicolaus Copernicus) heliocentrinio pasaulio modelio idėjas suformulavo apie 1505–1510 m. Visą heliocentrinio pasaulio teoriją jis aprašė svarbiausiame savo veikale „Apie dangaus sferų sukimąsi“, kuris buvo išspausdintas 1543 m., t. y. jo mirties metais. 2.9.5 pav. pavaizduota šiame veikale pateiktos heliocentrinės sistemos schema. Jo teorija natūraliai ir paprastai paaiškino Saulės ir planetų judėjimą. Remiantis šia teorija, buvo galima apskaičiuoti teisingus santykinius planetų atstumus nuo Saulės ir jų orbitinius (žvaigždinius) periodus. Šių dydžių neįmanoma apskaičiuoti remiantis geocentriniu Ptolemajo modeliu. Tačiau Koperniko teorija dar rėmėsi senomis klaidingomis prielaidomis, kad planetų orbitos turi būti apskritimai, kuriomis planetos juda tolygiai. Todėl pagal jo modelį apskaičiuojamos planetų padėtys nebuvo tikslesnės, palyginti su Ptolemajo modeliu.

2.9.5 pav. Mikalojus Kopernikas

Planetos orbitinis periodas

Uždavinys. Hipotetinės planetos sinodinis periodas S = 3 (Žemės) metai. Koks šios planetos apskriejimo aplink Saulę (žvaigždinis) periodas (P)?

Sprendimas

Sąlygoje nenurodyta, ar hipotetinė planeta yra vidinė, ar išorinė Žemės orbitos atžvilgiu. Todėl nagrinėsime abu atvejus. Jei planeta išorinė, taikome sinodinio judėjimo (2.9.1) lygtį;

1P=1P⊕-1S'

P=P⊕SS-P⊕=1·33-1=1,5 (metų).

Jei planeta vidinė, taikome sinodinio judėjimo (2.9.2) lygtį:

1P=1P⊕+1S.

P=P⊕SS+P⊕=1·33+1=0,75  (metų).

Jupiterio opozicijos

Uždavinys. Jupiteris buvo stebimas opozicijoje vienų metų birželio 20 d. Kokiame žvaigždyne tuo metu buvo matomas Jupiteris? Po kiek laiko turėtų įvykti kita artimiausia Jupiterio opozicija? Kokia tai bus data?

Jupiterio orbitinis (žvaigždinis) periodas 4333d. Žemės orbitinis (žvaigždinis) periodas 365,3d.

Sprendimas

Birželio 20–21 d. yra vasaros saulėgrįžos dienos. Vadinasi, Saulės rektascensija α ≅ 6h 0m. Jupiteris yra opozicijoje, vadinasi, jo rektascensija α ≅ 6h + 12h = 18h. Ties šia rektascensija ekliptika eina Šaulio žvaigždynu. Taigi, Jupiteris tuo metu buvo Šaulio žvaigždyne.

Kita Jupiterio opozicija turi įvykti praėjus vienam sinodinio periodo laikotarpiui. Kadangi Jupiteris yra išorinė planeta Žemės atžvilgiu, jo sinodinį periodą skaičiuojame pagal (2.9.1) formulę:

1S=1P⊕+1P'

S≡PP⊕P-P⊕=4333·365,34333-365,3≅399d

Gauta sinodinio periodo trukmė ilgesnė už vienerius metus. Praėjus metams (arba 365d), bus vėl birželio 20 d. Prie šios datos dar turime pridėti 399 – 365 = 34 dienas. Taigi, kita Jupiterio opozicija bus praėjus vieneriems metams ir 34 dienoms, t. y. liepos 24 d.

Klausimai ir užduotys

  1. Ar įmanoma iš Marso stebėti Žemę, kai jis yra jos atžvilgiu jungtyje?
  2. Ar gali Venera atsidurti opozicijoje? Atsakymą pagrįskite.
  3. Koks yra Marso kampinis nuotolis nuo Saulės stebėtojui, esančiam Žemėje, kai Venera yra didžiausioje rytų elongacijoje tiek stebint iš Marso, tiek iš Žemės? Pavaizduokite aprašytą situaciją brėžiniu (tarkime, kad Veneros, Žemės ir Marso orbitos yra apskritiminės).
  4. Išorinės Saulės sistemos planetos sinodinis periodas S = 367,5 dienos. Raskite šios planetos orbitinį periodą.
  5. Marsas buvo stebimas opozicijoje kovo 21 d. Kokiame žvaigždyne tuo metu buvo matomas Marsas? Po kiek laiko turėtų įvykti kita eilinė Marso opozicija? Kuri tai bus data? Marso orbitinis (žvaigždinis) periodas 687,0d. Žemės orbitinis (žvaigždinis) periodas 365,3d. Išnagrinėkite galimas planetų konfigūracijas naudodamiesi programėle. Nustatykite planetos padėtį orbitoje stebėtojo planetos atžvilgiu, kad planeta būtų vienoje iš šių konfigūracijų: rytų kvadratūroje, jungtyje, opozicijoje, rytų elongacijoje, viršutinėje jungtyje.
  6. Išnagrinėkite regimąjį planetų judėjimą ir nustatykite jų konfigūracijas naudodamiesi virtualaus dangaus
    ​programomis.

Virtualaus dangaus programos:

Celestia

Stellarium

Daugiau
Daugiau pasirinkimų

Skyriaus „Praktiniai astronomijos pagrindai“ santrauka

  • Žvaigždynas yra apibrėžtas dangaus sferos plotas, kuriame yra į jį besiprojektuojančių šviesesnių žvaigždžių grupė, sudaranti kokią nors įsimintiną geometrinę figūrą, gyvūną arba mitologinį subjektą.
  • Šviesulio ryškis yra jo spindesio matas. Šviesulio spindesio ir ryškio sąryšis apibūdinamas Pogsono formule (žr. (2.2.2) formulę).
  • Dangaus sfera yra įsivaizduojama neapibrėžto spindulio sfera, kurios centras yra stebėtojo taške ir kurios paviršiuje yra projektuojamos visų dangaus šviesulių regimosios padėtys. Dangaus sferą apibūdina šie elementai: dangaus pusiaujas ir dienovidinis, dangaus šiaurės ir pietų poliai, zenitas, nadyras, horizonto plokštuma. Jos parinis sukimasis yra Žemės ašinio sukimosi atspindys.
  • Šviesulio padėtis dangaus sferoje gali būti apibūdinama dviem būdais: horizonto plokštumos atžvilgiu (aukštis h ir azimutas A) arba dangaus pusiaujo atžvilgiu (rektascensija α ir deklinacija δ).
  • Dėl Žemės sukimosi ašies precesijos iš lėto kinta dangaus polių ir pusiaujo padėtis žvaigždžių atžvilgiu. Dėl to keičiasi ir dangaus šviesulių pusiaujinės koordinatės.
  • Dangaus poliaus aukštis virš horizonto yra lygus vietovės geografinei platumai.
  • Regimasis šviesulio perėjimas per dangaus dienovidinį vadinamas šviesulio kulminacija. Viršutinė kulminacija būna tada, kai šviesulys pereina dienovidinį arčiausiai zenito, o apatinė kulminacija – kai šviesulys pereina dienovidinį arčiausiai nadyro.
  • Saulės centro viršutinės kulminacijos momentas vadinamas tikruoju vidurdieniu, o apatinės kulminacijos momentas – tikruoju vidurnakčiu.
  • Didžiausias aukštis, į kurį gali pakilti šviesulys virš horizonto, priklauso nuo jo deklinacijos ir stebėjimo vietos platumos.
  • Regimasis Saulės disko centro takas per žvaigždėtą dangų vadinamas ekliptika. Svarbiausi jos taškai: pavasario ir rudens lygiadienių taškai bei vasaros ir žiemos saulėgrįžos taškai.
  • Atogrąžiniai metai yra laiko tarpas tarp gretimų vienas po kito vykstančių regimojo Saulės disko centro perėjimų per pavasario lygiadienio tašką.
  • Regimoji Mėnulio fazė priklauso nuo Mėnulio ir Saulės santykinės padėties Žemės atžvilgiu.
  • Sinodiniu mėnesiu vadinamas laiko tarpas tarp gretimų vienodų Mėnulio fazių.
  • Saulės užtemimas įvyksta tada, kai priešais Saulę praskriejančio Mėnulio metamas šešėlis (pusšešėlis) uždengia tam tikrą Žemės paviršiaus dalį.
  • Mėnulio užtemimas įvyksta tada, kai Mėnulis, judėdamas savo orbita, įskrieja į Žemės metamą šešėlį.
  • Tiesioginiai metodai atstumams iki astronominių objektų nustatyti yra lokacijos (radiolokacijos) ir paralakso metodai. Saulės sistemos objektų atstumams nustatyti taikomas radiolokacijos arba horizontinio paralakso metodas. Žvaigždžių ir kitų tolimų objektų atstumai nustatomi (metinio) paralakso metodu.
  • Astronomijoje vartojami atstumo vienetai: astronominis vienetas (au), parsekas (pc) ir šviesmetis (ly).
  • Žvaigždinė para yra laiko tarpas tarp dviejų viena po kitos įvykstančių pavasario lygiadienio taško vienvardžių kulminacijų tame pačiame dienovidinyje.
  • Tikroji saulinė para yra laiko tarpas tarp dviejų viena po kitos įvykstančių regimojo Saulės disko centro vienvardžių kulminacijų tame pačiame dienovidinyje. Praktiniams poreikiams naudojama vidutinė saulinė para, kurios trukmė pastovi ir yra lygi tikrųjų saulinių parų vidurkiui.
  • Vietinis laikas – laikas, išmatuotas konkrečioje geografinėje ilgumoje (konkrečiame dienovidinyje).
  • Pasaulinis laikas (UT) – nulinio dienovidinio (λ = 0) vietinis vidutinis saulinis laikas.
  • Pasaulinis koordinuotasis laikas (UTC) – tarptautiniu mastu naudojamas civilinis pasaulinis lai kas, suderintas su atominiu ir pasauliniu laiku. Juostinis laikas – valandinės juostos centrinio dienovidinio koordinuotasis saulinis laikas.
  • Kalendorius – ilgų laikotarpių skaičiavimo sistema, kurioje nustatyta tam tikra mėnesių trukmė, jų metinis eiliškumas ir metų skaičiavimo pradžios momentas. Šiuo metu naudojamas Grigaliaus kalendorius yra Saulės kalendorius, pagrįstas atogrąžiniais metais.
  • Vidinių (Žemės atžvilgiu) planetų svarbiausios konfigūracijos: apatinė jungtis, viršutinė jungtis, didžiausios rytų ir vakarų elongacijos.
  • Išorinių (Žemės atžvilgiu) planetų svarbiausios konfigūracijos: jungtis, opozicija, rytų ir vakarų kvadratūros.
  • Sinodinis periodas (S) yra laiko tarpas tarp gretimų vienas po kito įvykstančių planetos perėjimų per tą pačią konfigūraciją.
  • Orbitinis, arba žvaigždinis, periodas (P) yra laiko tarpas, per kurį planeta vieną kartą apskrieja Saulę nejudančių žvaigždžių atžvilgiu.
  • Planetos sinodinį ir žvaigždinį (orbitinį) periodus sieja sinodinio judėjimo lygtis (žr. (2.9.1) ir (2.9.2) formules).
  • Stebimosios planetų konfigūracijos teisingai paaiškinamos remiantis heliocentriniu pasaulio modeliu.
Daugiau
Daugiau pasirinkimų
Prašau palaukti