Absoliučióji paklaidà, santykinė paklaidà, reikšminiai skaitmenys, matãvimo cilindras, gradúotoji pipètė, Mòro pipètė, biurètė, matãvimo kòlba, dỹdžio standártinė išraiška, chèminė fòrmulė, chèminė lygtis.
Matavimo paklaidos
Tiriant medžiagas matuojamos jų savybės, kiekis. Tam naudojami prietaisai. Jokiu prietaisu neįmanoma ko nors išmatuoti absoliučiai tiksliai. Matuodami visada susiduriame su paklaidomis. Paklaidas lemia ir prietaiso ypatybės, ir tyrėjo įgūdžiai naudotis prietaisu.
Absoliučióji paklaidà Δx yra matavimo rezultato ir tikrosios matuojamo dydžio vertės skirtumo modulis.
Δx = |xišmatuotasis – xtikrasis|;
(1.1.1)
čia x – matuojamas dydis,
Δx – absoliučioji paklaida,
xišmatuotasis – išmatuotoji dydžio vertė,
xtikrasis – tikroji dydžio vertė.
Santykinė paklaidà η yra absoliučiosios paklaidos ir tikrosios dydžio vertės santykis.
Santykinė paklaida dažniausiai išreiškiama procentais:
(1.1.2)
čia η – santykinė paklaida (procentais).
1 pavyzdys
Mokinys tyrė 20 °C temperatūros vandeninį tirpalą, kuriame natrio chlorido masės dalis 15 %. Jis nustatė, kad šio tirpalo tankis yra 1,101 g/cm3. Chemijos žinyne nurodytas tokio tirpalo tankis 1,107 g/cm3. Kokia yra mokinio atlikto matavimo absoliučioji ir santykinė paklaida (procentais)?
Sprendimas
Žinyno pateikiamą vertę laikysime tikrąja tankio verte. Tankis žymimas raide ρ, tad formulėse vietoj x rašysime ρ.
Absoliučioji paklaida:
∆ρ = |ρišmatuotasis – ρtikrasis | = |1,101 g/cm3 –1,107 g/cm3| = 0,006 g/cm3.
Santykinė paklaida:
Atsakymas: absoliučioji paklaida 0,006 g/cm3, santykinė paklaida 0,5 %.
Reikšminiai skaitmenys
Tiek tiesioginius matavimų rezultatus (pavyzdžiui, masę, tūrį), tiek remiantis šiais rezultatais atlikto skaičiavimo rezultatus (pavyzdžiui, tankį) turime pateikti užrašydami tik vadinamuosius reikšminius skaitmenis.
Reikšminiai skaitmenys – tai visi abejonės nekeliantys dydžio skaitmenys ir pirmasis skaitmuo, kuriame gali būti paklaida.
2 pavyzdys
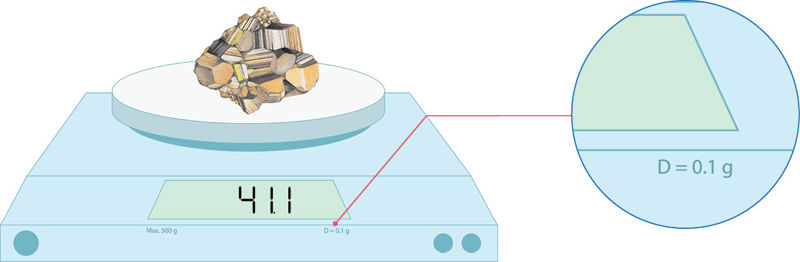
Ant elektroninių svarstyklių padėjus mineralo pirito (FeS2 ) pavyzdį, ekranėlyje įsižiebė užrašas 41,1 g (1.1.1 pav.). Svarstyklių apraše nurodyta, kad jų didžiausia absoliučioji paklaida yra ± 0,1 g. Keliais reikšminiais skaitmenimis išmatuota pirito masė?
Sprendimas
Kadangi svarstyklių paklaida yra ± 0,1 g, tikroji mineralo masė yra tarp:
41,1 g – 0,1 g = 41,0 g ir 41,1 g + 0,1 g = 41,2 g.
Pirmieji du skaitmenys (4 ir 1) nekelia abejonės, o paskutinis skaitmuo gali būti 0, 1 arba 2. Sakome, kad masę žinome trimis reikšminiais skaitmenimis.
Atsakymas: pirito masė žinoma trimis reikšminiais skaitmenimis.
Reikšminiai ir nereikšminiai nuliai
Net ir buitinėse situacijose frazės „susitikime devintą valandą“ ir „susitikime 9:00“ nėra lygiavertės. Antruoju atveju pabrėžiame susitikimo laiko tikslumą. Panašiai yra ir su laboratorinių matavimų rezultatais. Pavyzdžiui, skaičiai 137,8 ir 137,80 matematiškai yra lygiaverčiai, tačiau kaip matavimo rezultatas jie nėra vienodos vertės.
3 pavyzdys
Svarstyklės, kurių absoliučioji paklaida ± 0,01 g, rodo, kad skaičiuotuvo masė 137,80 g. Keliais reikšminiais skaitmenimis išmatuota skaičiuotuvo masė?
Sprendimas
Skaičiuotuvo masė žinoma 5 reikšminių skaitmenų tikslumu. Ji apima intervalą nuo 137,79 g iki 137,81 g.
Komentaras. Atkreipkite dėmesį, kad paskutinis skaitmuo – nulis – irgi yra reikšminis, nors ir žinomas su paklaida. Jį būtina užrašyti. Gale parašytas nulis rodo, kad paklaida skaičiuojama tik šimtosiomis gramo dalimis. Tarkime, svėrimo rezultatą užrašėme be paskutinio nulio, t. y. tiesiog 137,8 g. Toks užrašas reikštų, kad svarstyklių paklaida galėjo būti ± 0,1 g, o tikroji masė yra tarp 137,7 g ir 137,9 g.
Atsakymas: skaičiuotuvo masė žinoma penkiais reikšminiais skaitmenimis.
4 pavyzdys
Analizinių svarstyklių leidžiamoji paklaida yra ± 0,0001 g. Tokiomis svarstyklėmis pasverto cukraus kristalo masė 0,0100 g. Keliais reikšminiais skaitmenimis žinoma kristalo masė? Kurie svėrimo rezultato nuliai yra reikšminiai, o kurie ne?
Sprendimas
Jeigu svėrimo rezultatą išreikšime miligramais arba kilogramais, jis bus:
0,0100 g = 10,0 mg;
0,0100 g = 0,0000100 kg.
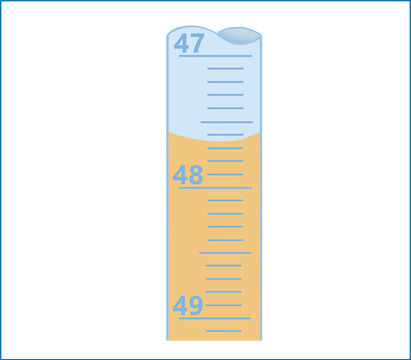
Išreiškus miligramais, priekyje buvusių nulių nebeliko. Išreiškus kilogramais, nulių priekyje pagausėjo. Priekyje esantys nuliai nėra reikšminiai. Jie atsiranda tik dėl pasirinktų matavimo vienetų, o ne dėl prietaiso tikslumo. Kiti du nuliai yra reikšminiai (1.1.2 pav.).
Atsakymas: kristalo masė žinoma trimis reikšminiais skaitmenimis.
Jei prietaisas ne elektroninis
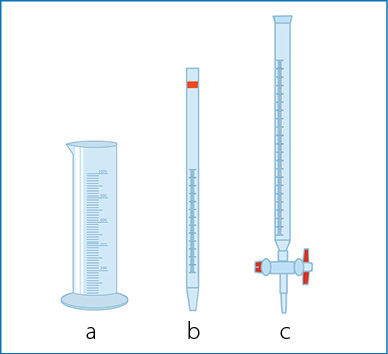
Visi elektroninių prietaisų ekrane rodomo matavimo rezultato skaitmenys, išskyrus priekinius nulius, yra reikšminiai. Matãvimo cilindras, biurètė, gradúotoji pipètė (1.1.3 pav.) ekrano neturi. Šie matavimo įrankiai turi skalę, panašią į liniuotės (1.1.4 pav.). Išsiaiškinkime, kaip šiuo atveju įvertinti reikšminių skaitmenų skaičių.
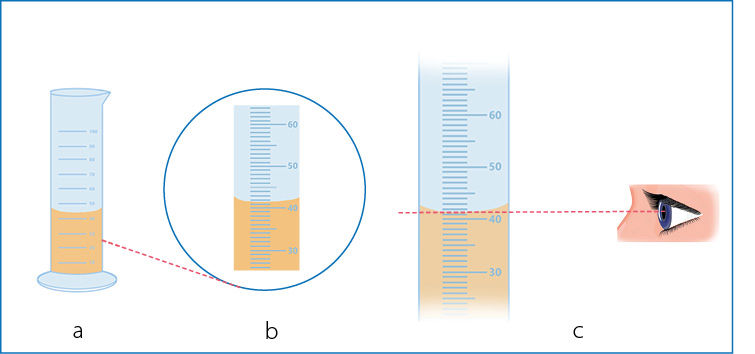
1.1.4 paveiksle (p. 11) matote matavimo cilindrą. Jame skysčio įpilta daugiau kaip 40 cm3, bet mažiau kaip 50 cm3. Pirmiausia išsiaiškiname, kokia yra vienos padalos vertė. Paveiksle intervalas tarp 40 ir 50 cm3 padalintas į 10 dalių. Vadinasi, vienos padalos vertė yra 1 cm3. Kadangi galime įvertinti, ar skysčio yra tiksliai ties mažiausia padala, ar šiek tiek tarp padalų, laikysime, kad šios matavimo priemonės absoliučioji paklaida yra pusės padalos vertės (šiuo atveju ± 0,5 cm3). Skysčio paviršius įgaubtas. Matuojame pagal žemiausią įgaubto paviršiaus tašką. Jis yra maždaug per vidurį tarp 41 ir 42 cm3. Tad skysčio tūris yra 41,5 cm3. Dėl pirmųjų dviejų skaitmenų (4 ir 1) abejonių nėra, o paskutinis skaitmuo įvertintas, kaip sakoma, „iš akies“. Pagal apibrėžimą, visi abejonės nekeliantys ir pirmasis abejotinas skaitmuo yra reikšminiai. Tad skysčio tūris išmatuotas trimis reikšminiais skaitmenimis. Ir nesvarbu, ar jį išreikšime kubiniais centimetrais (mililitrais), ar kubiniais decimetrais (litrais), o gal kubiniais metrais, reikšminių skaitmenų skaičius dėl to nepakis (skaičiaus priekyje atsirandantys nuliai nėra reikšminiai):
41,5 cm3 = 0,0415 dm3 = 0,0000415 m3.
Tam, kad nebūtų priekinių nulių, dydžius galima užrašyti standártine išraiška:
4,15 · 101 cm3 = 4,15 · 10–2 dm3 = 4,15 · 10–5 m3.
Jeigu skysčio būtų tiksliai sulig 41 padala, jo tūris būtų 41,0 cm3. Gale parašytas nulis yra reikšminis. Jis rodo, kad tik kubinio centimetro dešimtosios dalys įvertintos „iš akies“.
Biurečių skalė būna sugraduota dar smulkiau, dažniausiai kas 0,1 cm3 (1.1.5 pav.). Tad biuretės absoliučioji paklaida yra ± 0,05 cm3 (nebent ant paties prietaiso nurodyta kitaip). Naudodamiesi biurete atkreipkite dėmesį į toliau pateiktas pastabas.
- Biuretės nulinė padala yra viršuje, skaičiai didėja einant iš viršaus į apačią.
- Biuretė skirta ištekėjusio skysčio tūriui matuoti.
- Ištekėjusio skysčio tūris lygus galutinio ir pradinio rodmens skirtumui, t. y. dviejų matavimų skirtumui. Šių matavimų absoliučiosios paklaidos reikšmės sudedamos. Todėl iš biuretės ištekėjusio skysčio tūrio absoliučioji paklaida yra lygi ne pusės, o visos padalos vertei (2 · (± 0,05 cm3) = ± 0,1 cm3).
Matavimo kolba ir Moro pipetė
Tiksliems tūrio matavimams naudojamos matãvimo kòlbos ir Mòro pipètės (1.1.6 pav.) turi tik vieną padalą ir skirtos tik vienam tūriui matuoti. Paprastai tūris jomis matuojamas keturiais reikšminiais skaitmenimis. Tad jei matavimo kolba yra šimto kubinių centimetrų, rašome 100,0 cm3, o dvidešimt penkių kubinių centimetrų Moro pipetės tūris 25,00 cm3. Tą patį tūrį užrašius kitais matais, visi reikšminiai nuliai turi likti:
100,0 cm3 = 0,1000 dm3;
25,00 cm3 = 0,02500 dm3.
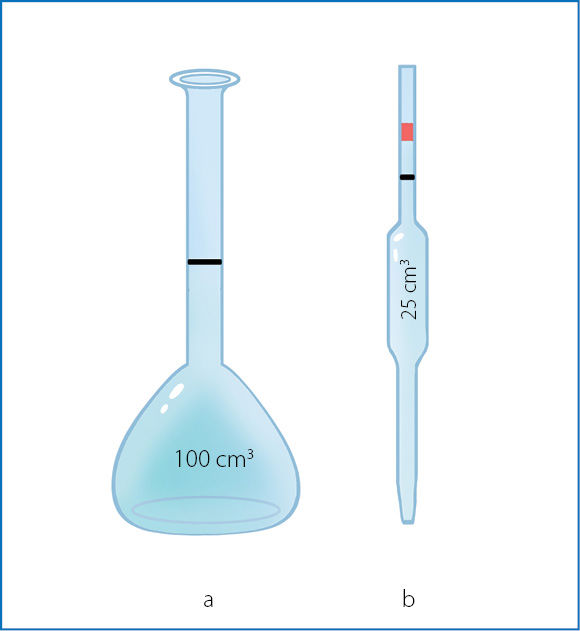
* Anglų literatūroje ši pipetė vadinama volumetric pipette (tūrio matavimo pipetė), o Moro (Mohr) pipete vadinama graduotoji pipetė.
1 m3 = 1000 dm3 = 1000 l.
1 dm3 = 1 l.
1 dm3 = 1000 cm3 = 1000 ml.
1 cm3 = 1 ml.
Klausimai ir užduotys
- Keliais reikšminiais skaitmenimis išreikšta masė arba tūris?
- 12,45 g;
- 12,00 g;
- 0,010500 kg;
- 0,01000 dm3;
- 10,0 cm3.
- Svarstyklių dokumentuose nurodyta, kad jų absoliučioji paklaida neviršija 0,01 g. Šiomis svarstyklėmis pasverti du metalo gabaliukai. Vieno masė 57,18 g, kito 3,47 g.
- Keliais reikšminiais skaitmenimis nustatyta vieno ir kito gabaliuko masė?
- Jei abiejų metalo gabaliukų absoliučioji paklaida 0,01 g, kokia yra vieno ir kito gabaliuko masės matavimo santykinė paklaida (procentais)?
- Bandymui reikia dvidešimt penkių kubinių centimetrų skysčio. Išrikiuokite toliau nurodytas tūrio matavimo priemones minėto tūrio matavimo tikslumo didėjimo tvarka.
- Matavimo cilindras, kurio mažiausios padalos sužymėtos kas 2 cm3;
- Moro pipetė, turinti tik vieną padalą ir skirta 25 cm3 tūriui;
- Biuretė, kurios mažiausios tūrio padalos sužymėtos kas 0,1 cm3;
- Cheminė stiklinė, kurios tūrio padalos pažymėtos kas 25 cm3.
- Service provided by UAB "Biznio mašinų kompanija" and "Star Cloud OÜ"