1 užduotis
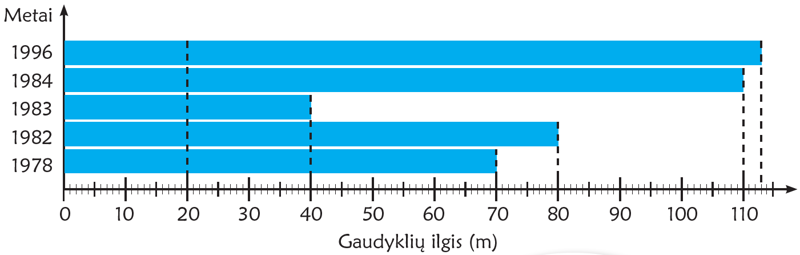
1. Lankydamiesi Ventės rage, vaikai sužinojo, kad pirmiausia yra pastatomos įvairių dydžių paukščių gaudyklės, o tik tada sugauti paukščiai žieduojami. Visos gaudyklės yra apie 10 m pločio ir apie 6 m aukščio. Skiriasi jų ilgis. Rokas diagrama pavaizdavo, kuriais metais kokio ilgio gaudyklės buvo pastatytos Ventės rage.
 | 1978 m. pastatyta gaudyklė buvo net 69 m pločio ir 25 m aukščio – tai didžiausia paukščių audyklė pasaulyje. |
- Kelintais metais buvo pastatyta ilgiausia gaudyklė?
- m.
- Kelintais trumpiausia?
- m.
- Kiek metrų ilgiausia gaudyklė ilgesnė už kiekvieną kitą gaudyklę?
Metai | Ilgis (m) | Skirtumas (m) |
1996 | ||
1984 | ||
1983 | ||
1982 | ||
1978 |
- Palyginkite didžiausios gaudyklės plotį ir aukštį su kitų gaudyklių aukščiu.
Paukščių gaudyklė | Aukštis (m) | Plotis (m) |
Didžiausia pasaulyje gaudyklė | ||
Įprasta gaudyklė | ||
Skirtumas |
2–3 užduotys
2. Juodoji zylė žiemoja Prancūzijoje. Ji nuskrenda apie 3500 km. Gervės žiemoti skrenda apie 2500 km. Palyginkite zylės ir gervės įveikiamą kelią. Kiek kilometrų daugiau nuskrenda juodoji zylė?
- 3500 km2500 km
Juodoji zylė nuskrenda km daugiau.
3. Įrašykite reikiamus skaičius ir palyginkite, pasirinkdami ženklą >, < ar = . Ką gausite kiekvienu atveju – lygybę ar nelygybę?
- 100 + 50 ir 200.
200, vadinasi, tai - 340 – 120 ir 200.
200, vadinasi, tai - 440 + 350 ir 610 + 180.
, vadinasi, tai - 260 + 130 ir 790 – 370.
, vadinasi, tai
|
Tarp dviejų skaičių ar tarp dviejų reiškinių parašę ženklą > arba < gauname nelygybę. |
 |
4–5 užduotys
4. Kiek minučių Rokas stebėjo paukščius antrą dieną?
Pirmą dieną stebėjau paukščius 40 min., o iš viso per dvi dienas – 100 min. |  |
40 + x = 100
x = 100 – 40
x =
|
Veiksmų eilutėje nežinomą skaičių pažymėję raide, gauname lygtį. |
 |
5. Išspręskite lygtis, t. y. apskaičiuokite, koks skaičius turi būti vietoj kiekvienos raidės, ir parašykite gautą atsakymą. Paaiškinkite, kaip apskaičiuoti nežinomą atėminį ir turinį.
- x + 210 = 360
x = - 470 + a = 890
a = - 634 + b = 976
b =
- 634 – c = 320
c = - 798 – y = 214
y = - a – 140 = 730
a = - x – 321 = 356
x =
Aš jau žinau. | O kaip apskaičiuosime nežinomą atėminį ir turinį? |
 | |
Nežinomą dėmenį nesunku apskaičiuoti, nes žinome, kad iš sumos atėmę vieną dėmenį, gauname kitą dėmenį. Pavyzdžiui: | |
- Paslaugą teikia UAB "Biznio mašinų kompanija" ir "Star Cloud OÜ"