Greičiai ir orbitos

Iš patirties žinote, kad tolyn mestas akmenukas po kurio laiko nukrinta, ir kuo didesnis jo pradinis greitis, tuo jis nuskrieja toliau. Nagrinėdamas tokį judėjimą Niutonas priėjo išvadą, kad suteikus kūnui pakankamai didelį greitį jis ant Žemės nebenukristų, bet ją apskrietų apskritimine trajektorija (4.3.1 pav.).

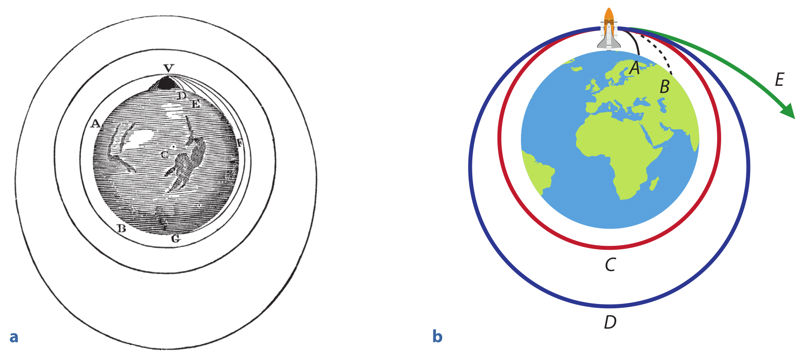
Apskritimine orbita skriejančio kūno greitį galima apskaičiuoti taip:

\nu=\sqrt{\frac{GM}{R}}. (4.3.1)

Kai orbitos spindulys R yra lygus kosminio kūno spinduliui (tariame, kad šis kūnas yra vienodo tankio rutulys), greitis, apskaičiuotas pagal (4.3.1) formulę, vadinamas pirmúoju kòsminiu greičiù.

Čia kalbame apie greitį, kurį turi orbitoje iš inercijos judantis objektas (pvz., palydovas arba raketa su išjungtais varikliais, 4.3.2 pav.).

Kad objektas, esantis Žemėje, įgytų pirmąjį kosminį greitį, jam reikia suteikti labai daug energijos. Šiuolaikinėse kosminėse raketose kuras sudaro daugiau kaip 90 % pradinės masės. Taupant energiją, raketą į kosmosą paprastai stengiamasi leisti Žemės sukimosi kryptimi ir iš tokios vietovės, kuri yra arčiau pusiaujo, nes taip startuojančios raketos pradinis greitis horizontalia kryptimi sutampa su Žemės paviršiaus greičiu, o jis yra didžiausias ties pusiauju.

Antrasis kosminis greitis yra apie 1,414 karto didesnis už pirmąjį kosminį greitį:

$$ {\nu }_2=\sqrt{\frac{2GM}{r}}=\sqrt{2}{v}_1.$$ (4.3.2)

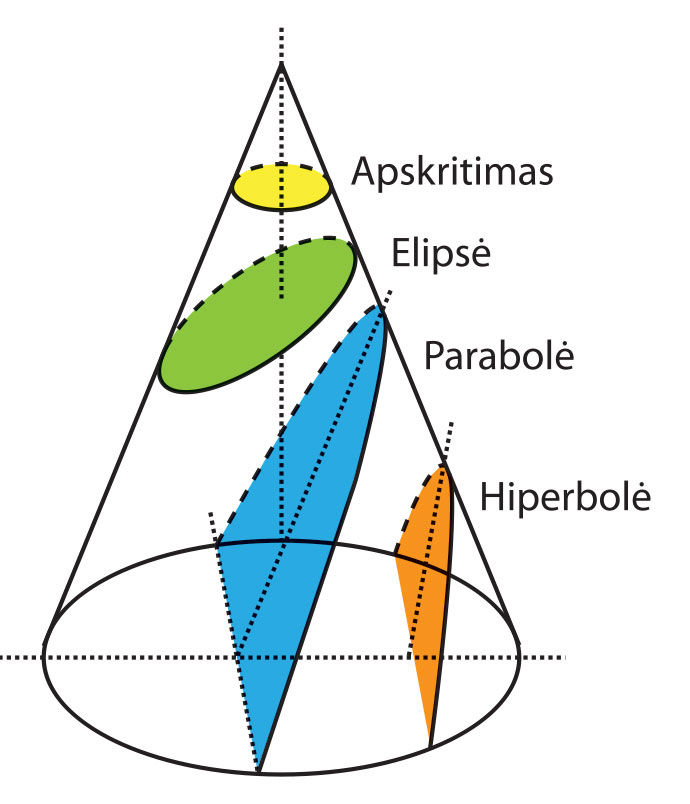
Apskritimas, elipsė, parabolė ir hiperbolė vadinamos kūgio pjūvio, arba antrõsios eilės, kreivėmis, nes jas galima gauti plokštuma įvairiais kampais kertant kūgį (4.3.4 pav.), o jų matematiniam aprašymui taikomos antrojo laipsnio funkcijos.

Kalbant apie kosminius skrydžius dar vartojamas terminas trečiàsis kòsminis greitis – tai mažiausias greitis, kurį įgijęs bet koks objektas – erdvėlaivis arba natūralus kosminis kūnas – gali ištrūkti iš Saulės sistemos traukos lauko (1 au atstumu nuo Saulės šis greitis lygus 42,1 km/s). Startuojant 200 km aukštyje nuo Žemės jos skriejimo kryptimi ir atsižvelgiant į Mėnulio gravitacijos poveikį trečiasis kosminis greitis Žemės atžvilgiu yra apie 16,6 km/s.

Orbitinį greitį bet kuriame orbitos taške galima apskaičiuoti remiantis mechãninės energijos tvermės dėsniu. Kai aplink M masės kūną skrieja m masės objektas, tai tokio objekto kinetinės (E_k) ir potencinės (E_p) energijos suma yra pastovus dydis:

$$ E_{\mathrm{k}}+E_{\mathrm{p}}=$$ $$ \mathrm{const}. \Rightarrow \frac{m{v}^{\mathit{2}}}{2}- G\frac{Mm}{r}=$$ $$ -G\frac{Mm}{2a};$$ (4.3.3)

čia a – objekto orbitos didysis pusašis; G – gravitacijos konstanta.

Pagal (4.3.3) formulę, kad nuotoliu r nuo centrinio kūno objekto greitis

\nu\left(r\right)\left[\mathrm{m}/\mathrm{s}\right]=\sqrt{GM\left[\mathrm{kg}\right]\left(\frac{2}{r\left[m\right]}-\frac{1}{a\left[m\right]}\right)}. (4.3.4)

Ši orbitinio greičio apskaičiavimo formulė vadinama νis-νiνa formule.

Jei centrinis kūnas – Saulė, o atstumai r ir a išreikšti astronominiais vienetais (au), tai

\nu\left(r\right)\left[\mathrm{\mathrm{k}m}/\mathrm{s}\right]=29,78\left[\mathrm{km}/\mathrm{s}\right]\sqrt{\frac{2}{r\left[\mathrm{au}\right]}-\frac{1}{a\left[\mathrm{au}\right]}}; (4.3.5)

čia koeficientas 29,78 km/s – vidutinis Žemės orbitinis greitis.

Elipse skriejančio objekto didžiausias galimas įgyti potencinės energijos kiekis yra didesnis už galimą įgyti didžiausią kinetinės energijos kiekį (|E_k| < |E_p|), o skriejančio hiperbole – mažesnis (|E_k| > |E_p|). Parabolinės orbitos atveju abu energijos kiekiai yra vienodi (|E_k| = |E_p|).