Reagúojančiosios mẽdžiagos, reãkcijos prodùktai, kiẽkių sántykis (moliais), reikšminiai skaitmenys, papildomi skaitmenys, išeiga, núostoliai, Avogãdro dėsnis, dùjų mòlinis tūris.
Skaičiavimai remiantis reakcijos lygtimi
Cheminė lygtis rodo reagúojančiųjų mẽdžiagų ir reãkcijos prodùktų kiekių sántykį. Panagrinėkime, kaip atliekami skaičiavimai remiantis chemine lygtimi ir kaip taikomos reikšminių skaitmenų taisyklės.
1 pavyzdys
Į 20,0 g nežinomos procentinės koncentracijos etano rūgšties tirpalo įdėjus magnio, išsiskyrė 0,34 dm3 dujų ir liko dalis nesureagavusio magnio. Dujų tūris nurodytas standartinėmis sąlygomis. Apskaičiuokite etano rūgšties procentinę koncentraciją tirpale.
Sprendimas
Išsiskiriančios dujos – tai vandenilis. Nurodyta, jog liko nesureagavusio magnio, vadinasi, etano rūgštis sureagavo visa. Medžiagos reaguoja taip:
(1.6.1)
Išsiskyrusio vandenilio kiekį randame pasinaudoję (1.4.3) formule (žr. p. 19):
Cheminė lygtis rodo, jog sureagavus 2 moliams etano rūgšties išsiskiria 1 molis vandenilio. Lygties koeficientai yra tikslūs skaičiai ir reikšminių skaitmenų skaičiaus neriboja.
Sudarome proporciją:
sureagavus 2 mol CH3COOH susidaro 1 mol H2,
sureagavus x mol CH3COOH susidaro 0,01498 mol H2;
Išsprendę gauname: x = 0,02995 mol CH3COOH.
M(CH3COOH) = 60,06 g/mol;
m(CH3COOH) = n · M = 0,02995 mol · 60,06 g/mol =
1,799 g.
Sudarome proporciją:
20,0 g – 100 %,
1,799 g – x %;
Atsakymas: etano rūgšties procentinė koncentracija – 9,0 %.
Komentaras. Sprendimuose atlikome tik daugybos ir dalybos veiksmus. Mažiausiai reikšminių skaitmenų – du – turi tūrio duomenys, todėl galutinis atsakymas suapvalintas iki dviejų reikšminių skaitmenų. Tarpiniuose atsakymuose palikome po du papildomus skaitmenis. Taip išvengėme apvalinimo paklaidų kaupimosi. Jeigu kiekviename sprendimo žingsnyje apvalinsime iki reikšminių skaitmenų, apvalinimo paklaidos gali susikaupti ir gerokai pakeisti rezultatą.
2 pavyzdys
Į 100,00 cm3 druskos rūgšties tirpalo įdėta 15,425 g aliuminio skardos ir palaikyta, kol nustojo skirtis dujos. Pasibaigus reakcijai likusi skarda nuplauta, išdžiovinta ir pasverta. Jos masė 15,025 g. Apskaičiuokite druskos rūgšties molinę koncentraciją pradiniame tirpale.
Sprendimas
(1.6.2)
Apskaičiuosime sureagavusio aliuminio masę: 15,425 g – 15,025 g = 0,400 g.
Pradinė ir galutinė masė žinoma penkiais reikšminiais skaitmenimis. Sureagavusio aliuminio masė žinoma trimis reikšminiais skaitmenimis. Atimant reikšminių skaitmenų skaičius gali sumažėti.
Iš cheminės lygties matome, kad druskos rūgšties, skaičiuojant moliais, sureaguoja 3 kartus daugiau negu aliuminio. Jei iš karto to nematote, sudarykite proporciją, kaip 1 pavyzdyje. Skaičius 3 yra tikslus, todėl tolesnių skaičiavimų reikšminių skaitmenų skaičiaus nekeičia.
n(HCI) = 3 ⋅ 0,014826 mol = 0,044477 mol;
Atsakymas: c(HCl) = 0,445 mol/l.
Išeiga
Iš patirties žinome, kad ką nors gaminant būna nuostolių. Dėl įvairių priežasčių reakcijos produktų gali pavykti surinkti mažiau, nei apskaičiuota pagal reakcijos lygtį. Dėl įrangos nesandarumo galimi dujų nuostoliai. Surenkant nuosėdas dalis jų lieka prilipusi prie indo sienelių. Gali vykti šalutinės reakcijos, susidaryti kitų produktų. Kokią dalį pagal cheminę lygtį apskaičiuoto reakcijos produkto pavyko gauti, rodo išeiga. Ją paprastai išreiškiame procentais ir skaičiuojame sudarydami proporcijas arba remdamiesi kuria nors formulių:
(1.6.3)
(1.6.4)
(1.6.5)
čia η – išeiga, nf, mf, Vf – faktiškai surinktas reakcijos produkto kiekis, masė arba tūris, nt, mt, Vt – teorinis (apskaičiuotas remiantis reakcijos lygtimi) reakcijos produkto kiekis, masės arba tūris.
3 pavyzdys
1,2 · 10–4 mol etanalio veikiant sidabro oksido amoniakinio tirpalo pertekliumi, ant mėgintuvėlio sienelių susidarė sidabro danga. Tuščio mėgintuvėlio masė prieš bandymą 12,345 g, o jo masė su sidabro danga 12,368 g. Apskaičiuokite sidabro išeigą procentais.
Sprendimas
(1.6.6)
Arba galima apskaičiuoti sudarant proporciją:
Atsakymas: sidabro išeiga – 89 %.
Tarkime, reikia pagaminti užsakytą reakcijos produkto kiekį. Jeigu yra nuostolių, reaguojančiųjų medžiagų teks imti daugiau, nei apskaičiuota pagal reakcijos lygtį. Taip nuostolius galima kompensuoti.
4 pavyzdys
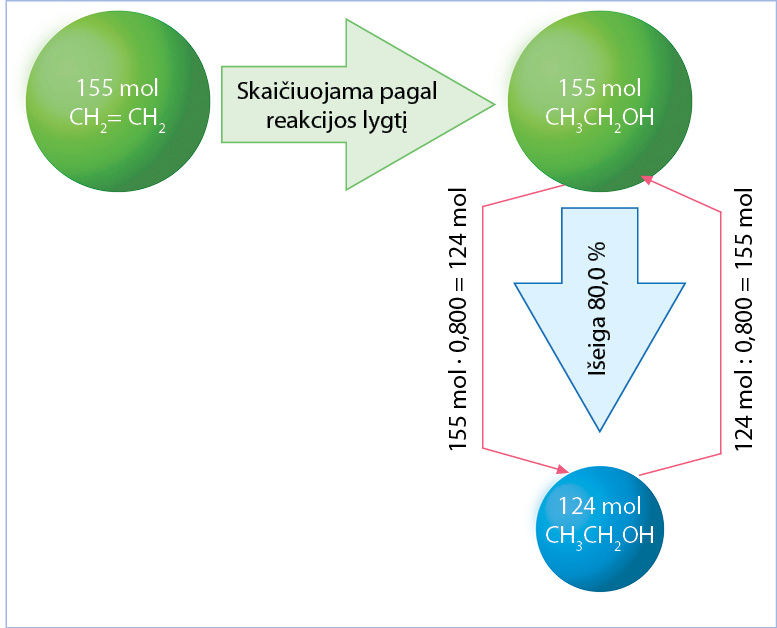
Įmonė etanolį gamina eteną veikdama vandeniu. Reakcija vyksta esant aukštai temperatūrai ir naudojant katalizatorius. Etanolio išeiga – 80,0 %. Kiek molių eteno sunaudojama gaminant 124 mol etanolio?
Sprendimas
CH2= CH2(d) + H2O(d) → CH3CH2OH(d).
(1.6.7)
Iš formulės
n(eteno) = n(etanolio) = 155 mol.
Atsakymas: 155 mol eteno.
Komentaras. Jei nebūtų nuostolių, reikėtų 124 mol eteno. Nuostoliams kompensuoti jo tenka naudoti daugiau (1.6.1 pav.).
Avogadro dėsnis
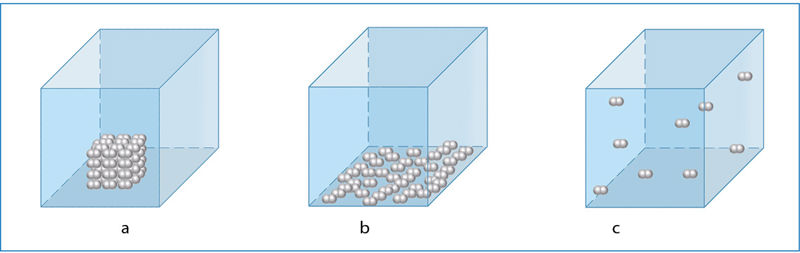
Kietosiose medžiagose ir skysčiuose molekulės yra arti viena kitos, todėl medžiagos užimamas tūris priklauso ir nuo molekulių dydžio, ir nuo jų išsidėstymo tvarkos. Dujose atstumai tarp molekulių daug didesni už pačių molekulių matmenis, todėl molekulių dydis neturi įtakos medžiagos užimamam tūriui (1.6.2 pav.). Dujoms galioja Avogãdro dėsnis, suformuluotas Amadėjaus Avogadro (Amedeo Avogadro, 1776–1856).
Vienodame įvairių dujų tūryje vienodomis sąlygomis yra vienodas molekulių skaičius.
Vienodos sąlygos – tai vienoda temperatūra ir slėgis. Svarbiausios šio dėsnio išvados:
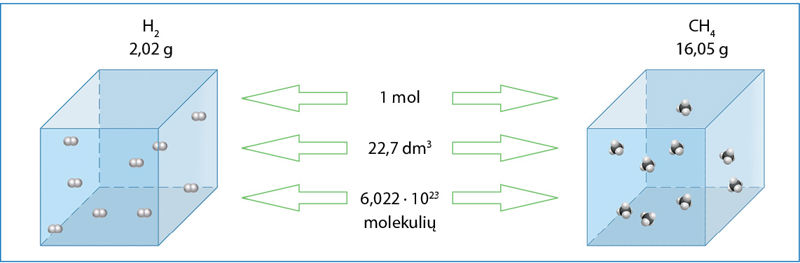
- 1 mol bet kurių dujų vienodomis sąlygomis užima vienodą tūrį. Standartinėmis sąlygomis (temperatūra 0 °C, o slėgis 100 000 Pa, arba 1 bar) šis tūris yra 22,7 dm3 (1.6.3 pav.). Jis vadinamas dùjų mòliniu tūriù, Vm = 22,7 dm3/mol.
- Reakcijos lygties dujinių medžiagų koeficientai rodo ne tik kokiu molių santykiu, bet ir kokiu tūrių santykiu reaguoja medžiagos. Ši išvada galioja ne tik standartinėmis sąlygomis.
5 pavyzdys
Apskaičiuokite deguonies ir oro, sunaudojamo degant 2,50 dm3 propano, tūrį. Dujų tūris matuojamas vienodomis sąlygomis. Deguonies tūrio dalis ore – 20,95 %. Degimo produktai yra anglies dioksidas ir vanduo.
Sprendimas
C3H8(d) + 5O2(d) → 3CO2(d) + 4H2O(s).
(1.6.8)
Remiantis Avogadro dėsniu, reakcijai reikalingo deguonies tūris yra 5 kartus didesnis už propano tūrį, jei tūriai matuojami vienodomis, nebūtinai standartinėmis, sąlygomis (1.6.4 pav.).
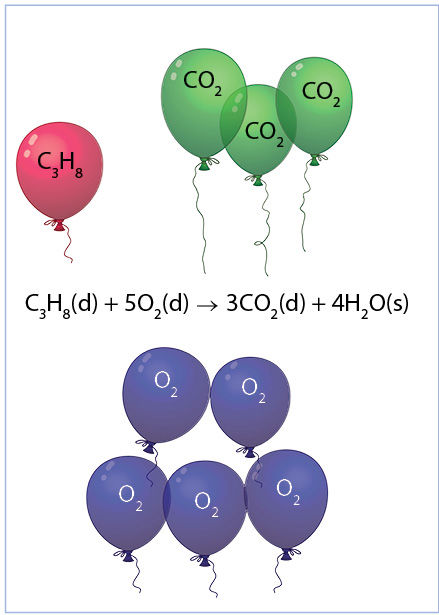
1.6.4 pav. Dujų tūrių santykis. Propano degimo reakcijos lygtis rodo, kad vienam propano tūrio vienetui reikia penkių deguonies tūrio vienetų, o anglies dioksido susidaro trys tūrio vienetai. Vanduo susidaro skystas, tad jam šis dėsningumas negalioja.
V(O2) = 5 · V(C3H8) = 5 · 2,50 dm3 = 12,5 dm3.
Oro tūriui apskaičiuoti sudarome proporciją:
12,5 dm3 – 20,95 %,
V(oro) – 100 %;
Atsakymas: deguonies reikia 12,5 dm3, oro – 59,7 dm3.
Klausimai ir užduotys
- Geležiai reaguojant su chloro dujomis Cl2, susidaro geležies(III) chloridas FeCl3. Parašykite geležies ir chloro reakcijos lygtį ir nurodykite:
- kokiu kiekių (moliais) santykiu reaguoja geležis ir chloras;
- kokiu masių santykių reaguoja šios medžiagos.
- Reaguojant vandeniliui H2 ir chlorui Cl2, susidaro vandenilio chlorido HCl dujos.
- Kiek molių chloro sunaudojama gaminant 125 mol vandenilio chlorido, jeigu jo išeiga 100 % ir jei
- Kiek litrų chloro sunaudojama gaminant 125 litrus vandenilio chlorido, jeigu jo išeiga 100 % ir jei 95 %? Dujų tūriai matuojami vienodomis sąlygomis.
- Geležinė detalė, kurios masė 45,283 g, pamerkta ir palaikyta druskos rūgšties tirpale. Ištrauktos, nuplautos ir išdžiovintos detalės masė 45,243 g. Geležiai reaguojant su druskos rūgštimi, susidaro geležies(II) chloridas. Apskaičiuokite išsiskyrusio vandenilio: a) masę; b) tūrį standartinėmis sąlygomis.
- Į 248,376 g masės cheminę stiklinę įpilta 155,463 g nežinomos koncentracijos druskos rūgšties tirpalo ir įdėta 5,483 g geležies. Nustojus skirtis dujoms cheminės stiklinės su joje esančiomis medžiagomis masė lygi 409,262 g. Apskaičiuokite išsiskyrusio vandenilio: a) masę; b) tūrį standartinėmis sąlygomis.
- Iš gamtinės sieros įmonė pagamino 1,0 · 106 kg 98 % sieros rūgšties. Nedegių priemaišų masės dalis gamtinėje sieroje siekia 5,0 %. Sieros rūgšties gamybos etapų supaprastinta schema:
Apskaičiuokite sunaudotos gamtinės sieros masę, jeigu:
- nėra gamybos nuostolių;
- sieros rūgšties išeiga – 85 %.
