Reiškiniai, lygtys, nelygybės

Kalbame apie reiškinius, lygtis, nelygybes.

1 užduotis

1. Įsižiūrėkite į korteles.

Kuriose lentelės dalyse jas padėtumėte? Sugrupuokite.

$\begin{matrix} 84 : (12 - 6) \end{matrix}$ $\begin{matrix} n + 2 = 5 \end{matrix}$ $\begin{matrix} b - 20 < 4 \end{matrix}$ $\begin{matrix} m : 2 = 44 \end{matrix}$ $\begin{matrix} a + 80 \end{matrix}$ $\begin{matrix} 80 > 10 \end{matrix}$

$\begin{matrix} n + 2 = 5 \end{matrix}$
$\begin{matrix} m : 2 = 44 \end{matrix}$
$\begin{matrix} 84 : (12 - 6) \end{matrix}$
$\begin{matrix} b - 20 < 4 \end{matrix}$
$\begin{matrix} a + 80 \end{matrix}$
$\begin{matrix} 80 > 10 \end{matrix}$

Prisiminkite ir aptarkite, ką žinote apie raidinius reiškinius, lygtis ir nelygybes su nežinomuoju.

Raidinis
reiškinys

Apskaičiuoti reiškinio reikšmę

Reiškinio reikšmė

Lygtis su nežinomuoju

Išspręsti
lygtį

Sprendinys

Nelygybė su nežinomuoju

Išspręsti
nelygybę

Sprendinys

Raidinio reiškinio a + 80 reikšmė priklauso nuo kintamojo a reikšmės.

Lygties m : 2 = 44 nežinomasis pažymėtas raide m.

Raidė reiškinyje vadinama kintamuoju, o lygtyje – nežinomuoju.

Daugiau

2 užduotis

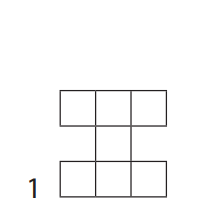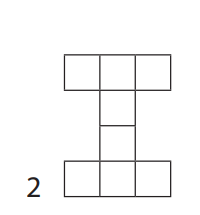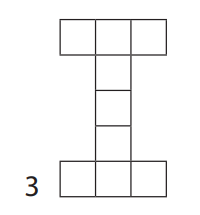2. Kiekvieną sekos figūrą sudaro tokio paties dydžio kvadratai. Pirmos trys figūros pavaizduotos.

Sugalvokite, kaip iš vienos figūros gauti kitą, po jos einančią.
Įsitikinkite, kad reiškinys 6 + m nusako, kiek langelių turi m vietoje esanti figūra.
Užpildykite lentelę.

Figūros numeris	Figūrą sudarančių langelių skaičius
1	6 + 1 = 7
2	6 + =
3

Kiek langelių užims 4-oji, 5-oji ir 6-oji šios sekos figūros?
- 4 figūra užims lang.
- 5 figūra užims lang.
- 6 figūra užims lang.
Yra žinoma, kad kažkuri šios sekos figūra turi 30 langelių. Kelinta tai figūra? Išspręskite lygtį: 6 + m = 30.
- m =
Koks bus figūros, turinčios 1 000 langelių, numeris?
- m =

Daugiau

3–5 užduotys gudručiams

3. Parašykite 3 sveikuosius skaičius, kuriuos įrašę vietoj x gautume teisingas skaitines nelygybes.

x > 16 · 5;
- , ,
x > 112 : 56;
- , ,

x < 12 · 56;
- , ,
1 696 : 4 < x
- , ,

4. Duota nelygybė: x > 12 · 56.

Raskite mažiausią sveikąjį skaičių, su kuriuo nelygybė yra teisinga.
Tik vieną iš parašytų reiškinių tiktų įrašyti x vietoje. Kurį? Paaiškinkite.

12 · 56
12 · 56 + 10
12 · 56 – 10
12 + 56

5. Jeigu apie kurį nors skaičių x yra žinoma, kad jis didesnis už 100, bet mažesnis už 105, tai galima parašyti dvigubą nelygybę su nežinomuoju: 100 < x < 105.
Parašykite teiginius dviguba nelygybe. Raskite visus sveikuosius skaičius, su kuriais tos nelygybės teisingos.