SĄVOKOS:
horizòntinės koordinãtės: aũkštis, ãzimutas, zenitinis núotolis, ekliptika, pavãsario lygiãdienio tãškas; pusiáujinės koordinãtės: rektasceñsija, deklinãcija, precèsija
Astronominės koordinatės
Jos naudojamos šviesulių padėtims dangaus sferoje nustatyti. Kaip žinote iš geografijos, bet kuri vieta Žemės paviršiuje nusakoma dviem kampiniais dydžiais (koordinatėmis): ilguma ir plãtuma. Panašiai ir astronomijoje: šviesulių padėtys dangaus sferoje taip pat nusakomos dviem kampais, bet šie kampai matuojami tam tikrų dangaus sferos plokštumų ir taškų atžvilgiu. Astronomai naudoja kelias koordinačių sistemas, o jos pasirenkamos, atsižvelgiant į sprendžiamus uždavinius. Šiame vadovėlyje išnagrinėsime dvi koordinačių sistemas: horizontinę ir pusiaujinę.
Horizontinė koordinačių sistema
Šioje sistemoje pagrindinė plokštuma yra horizonto plokštuma. Viena koordinatė, ãzimutas A, matuojama horizonto plokštumoje, o kita koordinatė, aukštis h, – statmenai horizonto plokštumai (2.4.1 pav.). Tuo tikslu per vertikalią liniją ZAZ’ ir šviesulį X išvedame plokštumą, kuri bus statmena horizonto plokštumai. Ši plokštuma kerta dangaus sferą pusapskritimiu ZXXHZ’, kuris vadinamas šviesulio vertikalù. Šviesulio aũkštis h yra kampas XHAX tarp horizonto ir krypties į šviesulį arba šviesulio vertikalo lanko XHX ilgis laipsniais. Šviesulio aukštis matuojamas nuo 0° iki +90° zenito kryptimi ir nuo 0° iki −90° nadyro kryptimi. Vietoj aukščio gali būti taikomas ir kitas dydis – zenitinis núotolis:
Tai yra kampas ZAX arba šviesulio vertikalo lanko ZX ilgis.
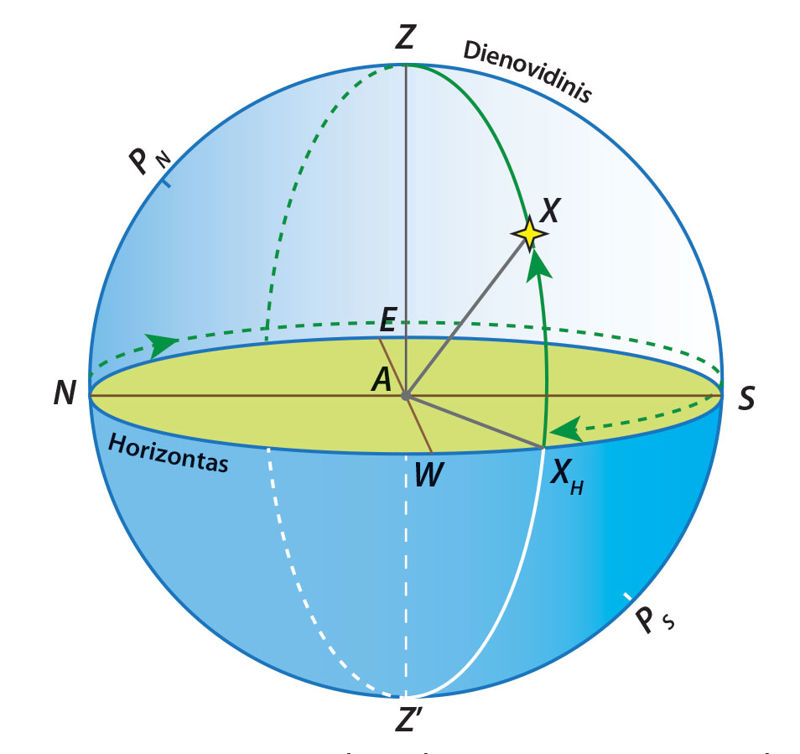
Kita koordinatė, ãzimutas3 A, yra kampas tarp dienovidinio šiaurės krypties N ir šviesulio vertikalo XHX arba lanko NESXH ilgis, kuris matuojamas išilgai horizonto linijos nuo šiaurės taško N4 rytų kryptimi (lankas NESWN) iki šviesulio vertikalo susikirtimo su horizontu taško XH. Azimutas matuojamas laipsniais nuo 0° iki 360°.
Horizontines koordinates patogu naudoti tada, kai norime stebėdami įvertinti šviesulių regimąsias padėtis horizonto atžvilgiu. Dėl parinio dangaus sferos sukimosi šviesulių horizontinės koordinatės nuolat keičiasi.
3 Ãzimutas [arab. as-sumūt – tiesus kelias, kryptis]
4 Kartais azimutas skaičiuojamas nuo pietų taško S vakarų kryptimi (lankas SWNES).
Klausimai ir užduotys
- Aldebarano aukštis virš horizonto h = 52°. Koks jo zenitinis nuotolis?
- Arktūro horizontinės koordinatės: aukštis virš horizonto h = 24°, azimutas A = 90°. Kurios pasaulio šalies kryptimi horizonto atžvilgiu bus matomas Aldebaranas?
- Alioto horizontinės koordinatės: aukštis virš horizonto h = 84°, azimutas A = 75°. Kuria kryptimi horizonto atžvilgiu bus matomas Aliotas?
- Kokiame aukštyje yra Saulė, jei vertikalaus strypo metamo šešėlio ilgis yra du kartus ilgesnis už strypo ilgį?
- Panagrinėkite horizontinę koordinačių sistemą, naudodamiesi programėle „Stebėtojas“ (The Observer, angl. k.). Naudodamiesi šia programėlės animacija, raskite 2 ir 3 užduotyse nurodytų žvaigždžių padėtis.
Astronominė refrakcija
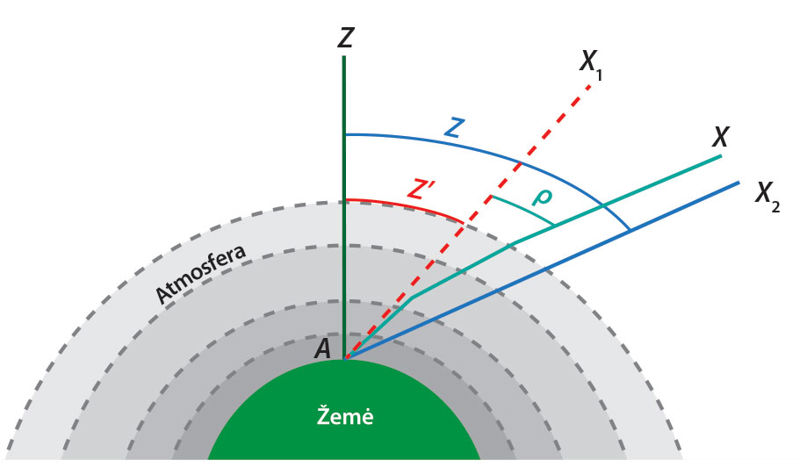
Apibūdinant horizontinės koordinačių sistemos koordinatès neatsižvelgiama į Žemės atmosferos įtaką. Iš tiesų dangaus kūno šviesos spinduliai pasiekia stebėtojo akį tik perėję per Žemės atmosferą. Šviesos spindulys, kuris pasiektų stebėtoją tam tikrame aukštyje virš horizonto, jei nebūtų atmosferos, pereidamas per atmosferą lūžta. Kadangi artėjant prie Žemės paviršiaus atmosferos tankis didėja, tai šviesos spindulys, artėjantis prie paviršiaus, vis labiau nukrypsta nuo savo pirminės krypties, ir stebėtojas mato šviesulį šiek tiek didesniame aukštyje (mažesniu zenitiniu nuotoliu), nei jis yra iš tikrųjų, kaip parodyta 2.4.2 pav. Žemėje esantis stebėtojas A mato šviesulį X ne kryptimi AX2, o šiek tiek aukščiau, kryptimi AX1. Šis šviesos spindulių sklidimo krypties pakitimas vadinamas astronòmine refrãkcija. Kampas X1AX2 vadinamas refrãkcijos kampù arba tiesiog refrãkcija ρ. Kampas ZAX2 yra tikrasis zenitinis nuotolis z, o kampas ZAX1 – regimasis zenitinis nuotolis z′. Iš brėžinio matome, kad
Refrakcijos dydis priklauso nuo šviesulio zenitinio nuotolio ir atmosferos slėgio bei temperatūros. Kai stebėtojo vietoje atmosferos slėgis lygus 1013,25 hPa, o temperatūra +10 °C, tai refrakciją galima apskaičiuoti pagal formulę
Ši formulė taikoma refrakcijai apskaičiuoti, kai z′ < 70°. Esant didesniems zenitiniams nuotoliams, refrakcijos vertės imamos iš specialių refrakcijos lentelių. Refrakcija ties horizontu (z′ = 90°) apytiksliai lygi 35′. Refrakcija neturi įtakos šviesulio azimutui. Refrakcija daro įtaką šviesulių tekėjimo ir leidimosi laikui. Dėl refrakcijos Mėnulio ir Saulės regimieji diskai ties horizontu atrodo šiek tiek suploti.
Pusiaujinė koordinačių sistema
Šioje sistemoje pagrindinė plokštuma yra dangaus pusiaujo plokštuma. Viena koordinatė, rektasceñsija5 α, matuojama pusiaujo plokštumoje, o kita koordinatė, deklinãcija6 δ, – statmenai pusiau jo plokštumai (2.4.3 pav.).
5 Rektasceñsija [lot. rectus + ascensio – status + pakilimas]
6 Deklinãcija [lot. declinatio – nuokrypis]
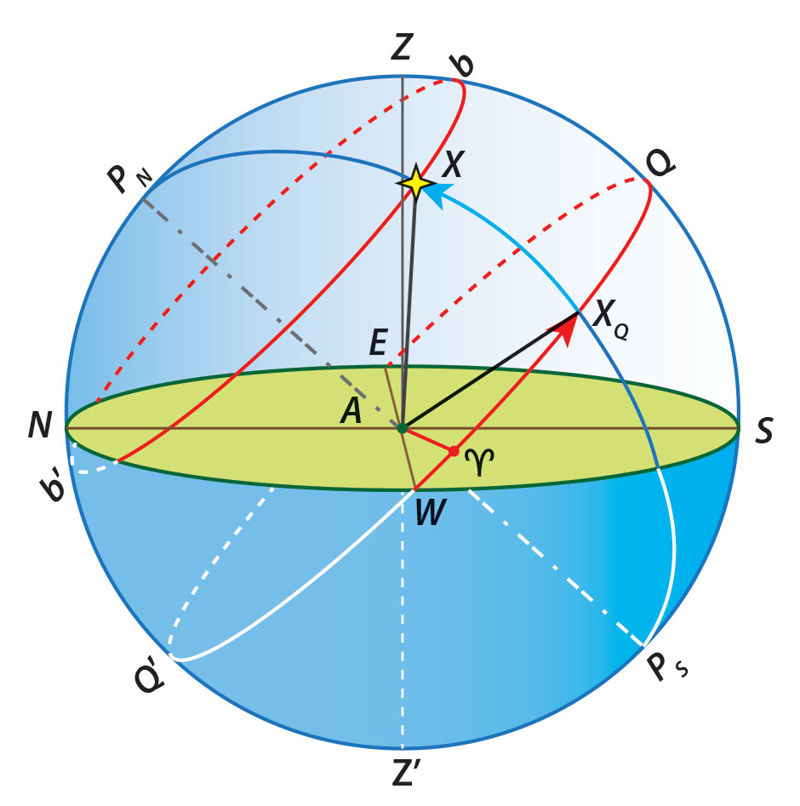
2.4.3 pav. Pusiaujinė koordinačių sistema, – pavasario lygiadienio taškas. Kiti žymenys – kaip pav. ir 2.4.1.
Koordinačių tinklą sudaro deklinacijų apskritimai (pusapskritimiai), jungiantys dangaus šiaurės ir pietų polius (PNXXQPS), ir dangaus lygiagretės, mažieji apskritimai, nubrėžti lygiagrečiai su dangaus pusiauju (Xbb’). Šviẽsulio deklinãcija δ yra kampas XAXQ tarp dangaus pusiaujo plokštumos ir krypties į šviesulį arba šviesulio deklinacijų pusapskritimio lanko XQX ilgis nuo dangaus pusiaujo iki šviesulio. Deklinacijos matuojamos nuo 0° iki +90° nuo pusiaujo dangaus šiaurės poliaus kryptimi ir nuo 0° iki −90° nuo pusiaujo dangaus pietų poliaus kryptimi. Kita koordinatė yra šviesulio rektasceñsija α. Jos atskaitos pradžia – dangaus pusiaujo taškas, vadinamas pavãsario lygiãdienio taškù . Šį tašką kerta Saulės regimojo judėjimo takas (ekliptika, žr. 2.6.1 skyrelį) kovo 20 arba 21 d. Taigi, šviẽsulio rektasceñsija α yra lankas XQ, matuojamas išilgai dangaus pusiaujo nuo pavasario lygiadienio taško iki deklinacijų apskritimo, arba kampas AXQ. Rektascensija matuojama nuo pavasario lygiadienio taško kryptimi, priešinga dangaus sferos regimajai sukimosi krypčiai (žvelgiant nuo dangaus šiaurės poliaus prieš laikrodžio rodyklę). Sukantis dangaus sferai ties dangaus pusiauju esantys šviesuliai teka (ir leidžiasi) vieni paskui kitus rektascensijos didėjimo eile. Paprastai rektascensijų vertės išreiškiamos ne kampo, o laiko vienetais. Per 24 val. dangaus sfera pasisuka 360°. Iš čia nesunku gauti rektascensijų, išreikštų laiko ir kampo vienetais, sąryšį. Laiko vienetai astronomijoje žymimi taip: valandos – h, minutės – m, sekundės – s. Šie vienetai rašomi prie skaičių kaip viršutiniai indeksai (laipsnio rodikliai). Pavyzdžiui, pavasario lygiadienio taško rektascensija užrašoma taip: α = 0h0m0,0s.
Kadangi pusiaujinių koordinačių atskaitos plokštumos ir taškai yra dangaus sferoje ir nesusiję su konkrečia stebėjimo vieta, tai šios koordinatės yra patogus būdas nurodyti bet kurio objekto vietą dangaus sferoje ar pažymėti žvaigždėlapyje. Pavyzdžiui, Vegos (Lyros α) pusiaujinės koordinatės yra tokios: α = 18h36m56,34s; δ = +38°47′01,3″.
Jei Žemės sukimosi ašies orientacija erdvėje būtų nekintanti, tai nesikeistų ir lygiadienių taškų padėtys dangaus pusiaujyje. Tačiau Žemė, veikiama Mėnulio ir Saulės gravitacijos, panašiai kaip besisukantis vilkelis, šiek tiek svyruoja. Todėl Žemės sukimosi ašis, lėtai judėdama erdvėje, apibrėžia kūgį. Tuo pat metu Žemės sukimosi ašies posvyris į jos orbitos plokštumą, lygus 66,56°, išlieka pastovus. Šis Žemės sukimosi ašies judėjimas, kurio periodas – apie 26 000 metų, vadinamas precèsija. Dėl to kinta dangaus polių ir pusiaujo padėtys žvaigždžių atžvilgiu. Dabartinė dangaus šiaurės poliaus kryptis beveik sutampa su Šiaurinės (Mažųjų Grįžulo Ratų α) padėtimi (atstumas tarp jų mažesnis nei 1°). Ilgainiui dangaus šiaurės polius atitols nuo Šiaurinės, ir ji nebeatitiks savo vardo. Po 5000 metų dangaus šiaurės polius bus ties Alderaminu (Cefėjo α), o po 12 000 metų – ties Vega (Lyros α). Kadangi dėl precesijos keičiasi dangaus poliaus ir pavasario lygiadienio taško padėtis danguje, tai atitinkamai keičiasi ir dangaus kūnų pusiaujinės koordinatės. Todėl užrašydami dangaus kūno pusiaujines koordinatès turime nurodyti ir laiko momentą (epochą), kada buvo išmatuota pavasario lygiadienio taško padėtis. Šiuo metu susitarta, kad kataloguose ir žvaigždėlapiuose objektų pusiaujinės koordinatės būtų nurodomos pagal 2000-ųjų metų pradžios pavasario lygiadienio padėtį. Todėl anksčiau pateiktas Vegos (Lyros α) pusiaujines koordinatès turėtume užrašyti nurodydami ir jų epochą: α(2000) = 18h36m56,34s; δ(2000) = +38°47′01,3″.
Precesija
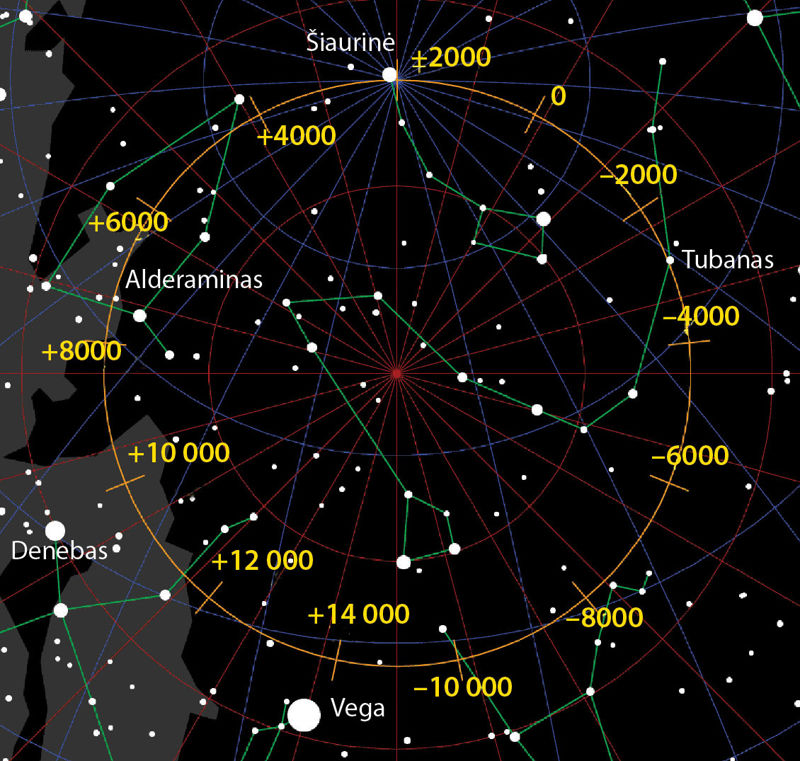
Kadangi Žemė yra šiek tiek susiplojusi per ašigalius, jos pusiaujo srityje yra daugiau masės negu ties ašigaliais. Dėl to Mėnulio ir Saulės gravitacija sukelia Žemės sukimosi ašies svyravimą, panašų į besisukančio vilkelio ašies svyravimą. Šis Žemės ašies svyravimas vadinamas precèsija. Žemės sukimosi ašis (dangaus polius) yra pasvirusi 23,44° kampu į statmenį savo orbitos plokštumai. Judėdamas apie šį statmenį dėl precesijos dangaus polius apibrėžia šio posvyrio kampo (t. y. 23,44°) spindulio apskritimą maždaug per 26 000 metų. Dėl precesijos keičiasi dangaus polių ir pusiaujo padėtys žvaigždžių atžvilgiu. Todėl lygiadienio taškai pasislenka Saulės regimojo judėjimo taku (ekliptika) į vakarus kasmet maždaug per 50″. Dangaus šiaurės poliaus precesinis judėjimas žvaigždžių fone parodytas 2.4.4 pav. Dabartinė dangaus šiaurės poliaus kryptis beveik sutampa su Šiaurinės (Mažųjų Grįžulo Ratų α) padėtimi. Bet prieš 4500 metų jis buvo Slibino žvaigždyne, šalia Tubano. Po 5000 metų jis bus ties Alderaminu (Cefėjo α), o po 12 000 metų – ties Vega (Lyros α).
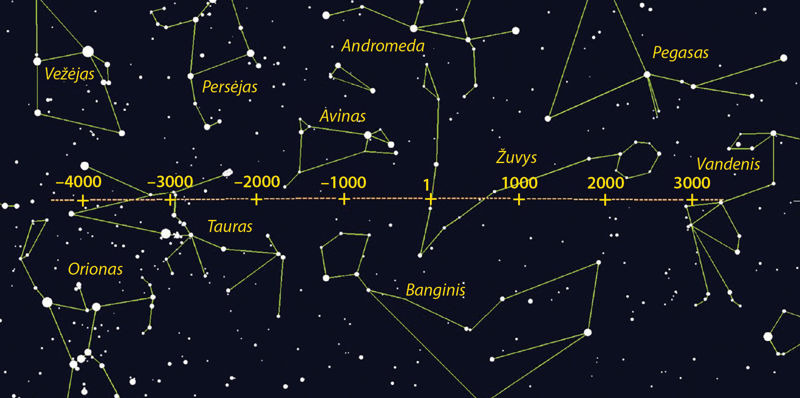
Pavasario lygiadienio taško slinkimas į vakarus žvaigždžių atžvilgiu parodytas 2.4.5 pav. Šiuo metu pavasario lygiadienio taškas slenka Žuvų žvaigždynu. Bet daugiau nei prieš 2000 metų pavasario lygiadienio taškas buvo Avino žvaigždyne. Iš tų laikų ir atėjo tradicija šį tašką žymėti Avino žvaigždyno simboliu (žr. taip pat 2.6.1 skyrelį). Pavasario lygiadienio taško precesinį judėjimą atrado senovės graikų mokslininkas Hiparchas II a. pr. Kr.
Klausimai ir užduotys
- Kokios būtų pusiaujinės koordinatės žvaigždės, esančios ant dangaus pusiaujo ir nutolusios per 45° į rytus nuo pavasario lygiadienio taško?
- Didžiausio regimojo spindesio žvaigždžių sąraše raskite žvaigždę, kuri būtų arčiausiai dangaus pietų poliaus. Kokiame ji žvaigždyne ir kokios jos pusiaujinės koordinatės?
- Žvaigždė matoma 8° nuotoliu nuo dangaus pietų poliaus. Kokia jos deklinacija?
- Panagrinėkite pusiaujines koordinates, naudodamiesi programėle „Pusiaujo koordinačių sistema“ (Equatorial Coordinate System, angl. k.). Nustatykite šių objektų pusiaujines koordinates: Kasiopėjos ir Didžiojo Šuns žvaigždynų, Vegos ir Kapelos (žvaigždžių).
Reiškiniai, susieti su dangaus sferos pariniu judėjimu
Ankstesniuose skyreliuose minėjome, kad netoli dangaus šiaurės poliaus matoma Šiaurinė tam tikroje geografinėje platumoje visą laiką būna maždaug vienodame aukštyje. Kad ir kokiame Žemės rutulio taške būtume, mes visada matysime parinį dangaus sferos sukimąsi aplink dangaus ašį, kuri yra lygiagreti su Žemės sukimosi ašimi. Tačiau pereinant vis į kitos geografinės platumos vietovę keičiasi vietinio horizonto ir dangaus poliaus tarpusavio padėtys. Dėl to keičiasi ir Šiaurinės aukštis, t. y. dangaus (šiaurės) poliaus aukštis virš horizonto priklauso nuo geografinės platumos. Ši priklausomybė apibūdinama taip: dangaus poliaus aukštis virš horizonto yra lygus vietovės geografinei platumai. Šią priklausomybę galima įrodyti remiantis 2.4.6 pav., kuriame schematiškai pavaizduota Žemės rutulio ir dangaus sferos projekcija į dangaus dienovidinio plokštumą. Dangaus poliaus aukštis virš horizonto hPN = ∡NAPN, o geografinė platuma φ = ∡ACq. Šie kampai lygūs, nes jų kraštinės statmenos viena kitai. Taigi, hPN = φ. Analogiškai: dangaus pietų poliaus aukštis yra lygus vietovės pietų platumai.
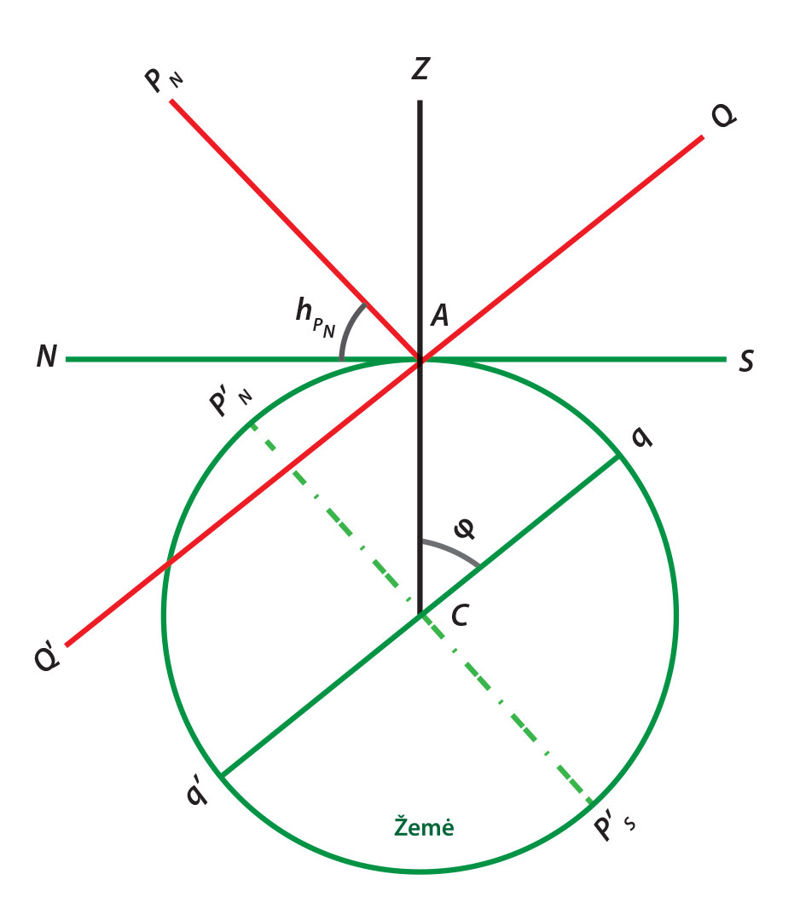
Vadinasi, jei norime nustatyti vietovės geografinę platumą, turime joje išmatuoti dangaus poliaus aukštį.
Kadangi Žemės pusiaujyje φ = 0°, tai ir dangaus poliaus aukštis virš horizonto hP = 0°, t. y. dangaus polius yra horizonte. Žemės ašigalyje φ = 90°, vadinasi, dangaus poliaus aukštis virš horizonto hP = 90°, t. y. dangaus polius yra zenite.
Kadangi keičiantis vietovės geografinei platumai keičiasi dangaus poliaus aukštis virš horizonto, tai ir regimasis dangaus sferos parinis sukimasis įvairiose platumose yra skirtingas.
Apžvelkime šviesulių judėjimą trijose platumose: 1) Žemės šiaurės ašigalyje, 2) vidutinėje šiaurės platumoje ir 3) Žemės pusiaujyje.
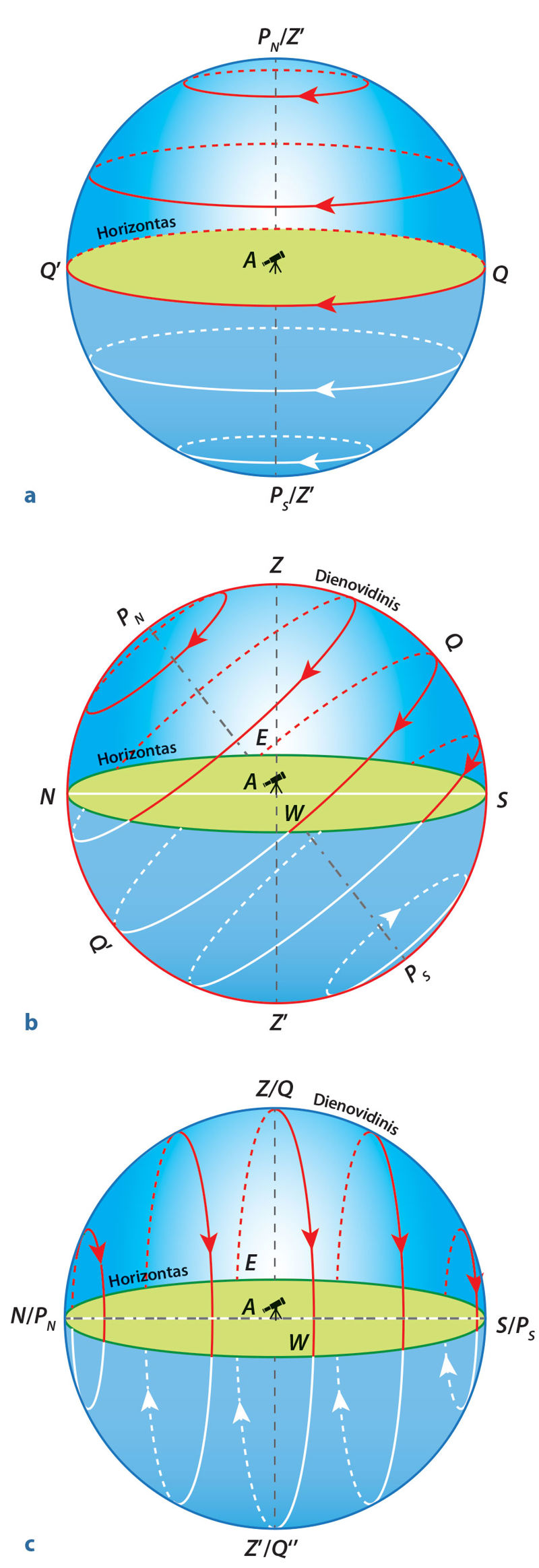
1) Žemės šiaurės ašigalyje dangaus polius bus zenite (2.4.7 pav., a). Šviesuliai judės koncentriškais apskritimais, lygiagrečiais su horizontu. Šviesuliai visą laiką matomi vienodame aukštyje; jie neteka ir nenusileidžia.
2) Vidutinėje šiaurės platumoje dangaus polius bus šiaurės pusėje geografinės platumos aukštyje (2.4.7 pav., b). Dangaus šiaurės poliaus aplinkoje matomi šviesuliai nenusileis, bet suksis ratu aplink jį. Tokie šviesuliai vadinami nenusiléidžiančiaisiais. Toliau nuo šiaurės poliaus matomi šviesuliai tekės horizonto rytų pusėje, pasieks aukščiausią pakilimo tašką virš horizonto ties dienovidiniu ir nusileis horizonto vakarų pusėje. Šviesulio tekà yra laiko momentas, kai kylantysis šviesulys kerta rytinio horizonto liniją. Šviesulio laidà yra laiko momentas, kai besileidžiantysis šviesulys kerta vakarinio horizonto liniją. Saulės ir Mėnulio tekõs laikas yra jų regimojo disko viršutinio krašto pakilimo virš rytinio horizonto momentas. Jų laidõs laikas yra jų regimojo disko krašto panirimo po vakariniu horizontu momentas. Kuo šviesuliai toliau nutolę nuo dangaus šiaurės poliaus, tuo jie trumpiau matomi virš horizonto. Žvaigždės, kurios yra dangaus pietų poliaus aplinkoje, visai nepatekės šioje platumoje. Tokie šviesuliai vadinami nepàtekančiaisiais.
3) Žemės pusiaujyje dangaus ašis guli horizonto plokštumoje (2.4.7 pav., c). Visi šviesuliai tekės ir leisis statmenai horizontui. Aukščiausią pakilimo tašką pasieks ties dienovidiniu. Jei išsklaidyta Saulės šviesa neužgožtų žvaigždžių, tai per parą būtų galima pamatyti visus dangaus žvaigždynus.
Per parą kiekvienas šviesulys savo dangaus lygiagrete apsisuka vieną kartą. Todėl jis du kartus pereina dangaus dienovidinį (žr. 2.4.7 pav., b ir c), jei nenagrinėsime atvejo, kai stebėtojas yra viename iš Žemės ašigalių.
Šviesulio perėjimas per dangaus dienovidinį vadinamas kulminãcija.
Viršutinė kulminãcija būna tada, kai šviesulys pereina dienovidinį arčiausiai zenito, o apatinė kulminãcija – kai šviesulys pereina dienovidinį arčiausiai nadyro. Jei tam tikroje platumoje šviesulys nenusileidžia žemiau horizonto, tai jis matomas virš horizonto abiejose kulminacijose.
Saulės centro viršutinės kulminacijos momentas vadinamas tikrúoju vidùrdieniu, o apatinės kulminacijos momentas – tikrúoju vidùrnakčiu.
Panagrinėjus 2.4.8 pav. nesunku įsitikinti, kad šviesulio deklinacija δ, aukštis virš horizonto h (zenitinis nuotolis z) ir stebėjimo vietos geografinė platuma φ – tarpusavyje susiję dydžiai. Jei šviesulys (X1 2.4.8 pav.) yra viršutinėje kulminacijoje į pietus nuo zenito, tai jo aukštis virš horizonto lygus
Jei šviesulys (X2 2.4.8 pav.) yra viršutinėje kulminacijoje į šiaurę nuo zenito, tai jo aukštis virš horizonto lygus
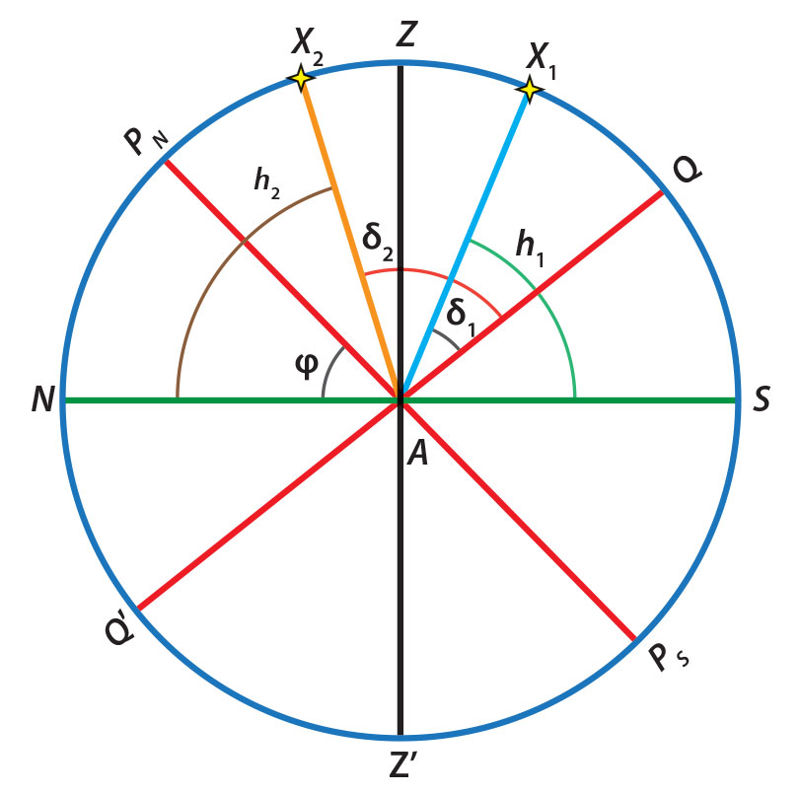
Šios formulės rodo, kad vietovės geografinę platumą galime apskaičiuoti, jei išmatuojame žvaigždės, kurios deklinacija žinoma, aukštį virš horizonto kulminacijos momentu.
Vietovės geografinė platuma
Uždavinys. Prokiono (α CMi, Mažojo Šuns α) aukštis viršutinės kulminacijos momentu Aleksándrijoje (Egiptas) lygus hA = 63°58′05″. Raskite Aleksándrijos geografinę platumą, jei Prokiono deklinacija δ = 5°09′58″.
Sprendimas
Pagal (2.4.2) formulę Prokiono aukštis Aleksándrijoje hA = 90° – φA + δ.
Iš čia Aleksándrijos platuma φA = 90° – hA + δ = 90° – 63°58′05″ + 5°09′58″ = 31°11′53″.
Žvaigždės aukštis viršutinės kulminacijos momentu
Uždavinys. Kokiame aukštyje virš horizonto bus matoma 1,8 ryškio žvaigždė Šaulio ε (ε Sgr) (δ = –34°22′) Drùskininkuose (φD = 54°01′ N)? Ar ši žvaigždė bus matoma viršutinės kulminacijos momentu Biržuose (φB = 56°12′ N)? Skaičiavimus atlikite: a) neatsižvelgdami į atmosferos refrakciją ir b) atsižvelgdami į atmosferos refrakciją.
Sprendimas
Žvaigždės aukštį viršutinės kulminacijos momentu neatsižvelgdami į refrakciją skaičiuojame pagal (2.4.2) formulę:
Druskininkuose: hD = 90° – 54°01′ – 34°22′ = 1°37′.
Biržuose: hB = 90° – 56°12′ – 34°22′ = – 0°34′. Aukštis neigiamas, vadinasi, žvaigždė nematoma.
Atsižvelgus į refrakciją žvaigždės aukštis Drùskininkuose h′D = 1°37′ + 0°35′ = 2°12′.
Biržuose h′B = – 0°34′ + 0°35′ = 0°01′. Žvaigždė horizonte taip pat nebus matoma.
Klausimai ir užduotys
- Kokia mažiausia deklinacija žvaigždės, kuri niekada nenusileidžia Kaũno geografinėje platumoje (φK = 54°54′)? Kokia bus ribinė deklinacija, jei bus atsižvelgta į atmosferos refrakciją ties horizontu?
- Dubės aukštis virš horizonto apatinės kulminacijos momentu h = 9°13′. Kokia vietovės geografinė platuma, jei Dubės deklinacija δ = 61°45′?
- Kokioje Žemės rutulio vietoje danguje matomi šviesuliai nei teka, nei leidžiasi?
- Kokia turėtų būti šviesulio deklinacija, kad jis patekėtų tiksliai rytuose ir nusileistų tiksliai vakaruose?
- Šiaurinės žvaigždės zenitinis nuotolis z = 55°. Kokia vietovės geografinė platuma?
- Naudodamiesi programėle panagrinėkite, kaip kinta šviesulių padėtys dangaus sferoje įvairiose geografinėse platumose. Programėlėje nustatykite savo vietovės geografines koordinates ir atsakykite į klausimus: ar visos žvaigždės pateka ir nusileidžia? Kurios žvaigždės visai nepateka šioje platumoje?
- Naudodamiesi programėle „Besisukančio dangaus tyrinėtojas (Rotating Sky Explorer, angl. k.), patyrinėkite parinį žvaigždžių judėjimą ties pusiauju ir ašigalyje. Kokius pastebite žvaigždžių judėjimo ypatumus?

