SĄVOKOS:
paralãksas, horizòntinis paralãksas, mẽtinis paralãksas, astronòminis vienetas, šviẽsmetis, parsèkas
Kaip matuojami astronominių objektų atstumai ir matmenys
Atstumai iki astronominių objektų labai dideli, todėl jie matuojami taikant nuotolinius atstumų nustatymo metodus. Vieni iš jų yra tiesioginiai metodai, ir papildomi duomenys apie nagrinėjamą objektą nereikalingi. Tai lokãcijos ir paralãkso metodai. Taikant netiesioginius metodus reikia papildomų duomenų apie objekto fizines savybes ar orbitinį judėjimą. Šiame skyriuje aptariami tik tiesioginiai metodai, o apie netiesioginius bus rašoma tolesniuose skyriuose.
Atstumų nustatymas lokacijos metodu
Lokacijos metodas – tai naujausias ir tiksliausias nuotolinio atstumo matavimo metodas. Jis paremtas tiksliai žinomu elektromagnetinių bangų (vadinasi, radijo bangų ir šviesos) sklidimo vakuume greičiu c. Metodas, kai lokacijai panaudojamas radijo bangų diapazonas, vadinamas radiolokãcijos metodù. Jį taikant matuojamas laiko intervalas t, per kurį iš Žemės pasiųstas radiolokacinis signalas, atsispindėjęs nuo tiriamojo dangaus kūno, grįžta į Žemę ir užregistruojamas radioteleskopu. Taigi, atstumas iki tiriamojo dangaus kūno lygus
Šiuo metodu galima nustatyti atstumus iki Saulės sistemos kūnų kietu paviršiumi. Remiantis šiuo metodu atliktais matavimais apibrėžtas ir tikslus astronominio vieneto (au) ilgis.
Tikslesnis už radiolokaciją yra lazerinės lokãcijos metodas. Tačiau jis taikytas tik atstumui nuo Žemės iki Mėnulio matuoti, nes tam, kad būtų efektyvesnis lazerio šviesos impulso atspindys, į Mėnulį reikėjo nugabenti specialius atšvaitus (retroreflèktorius).
Klausimai ir užduotys
- Iš Žemės į Venerą pasiųstas radiolokatoriaus signalas atsispindėjo nuo Veneros paviršiaus ir buvo užregistruotas Žemėje po 24m21,1s. Koks tada buvo Veneros atstumas nuo Žemės?
Atstumų nustatymas paralakso metodu
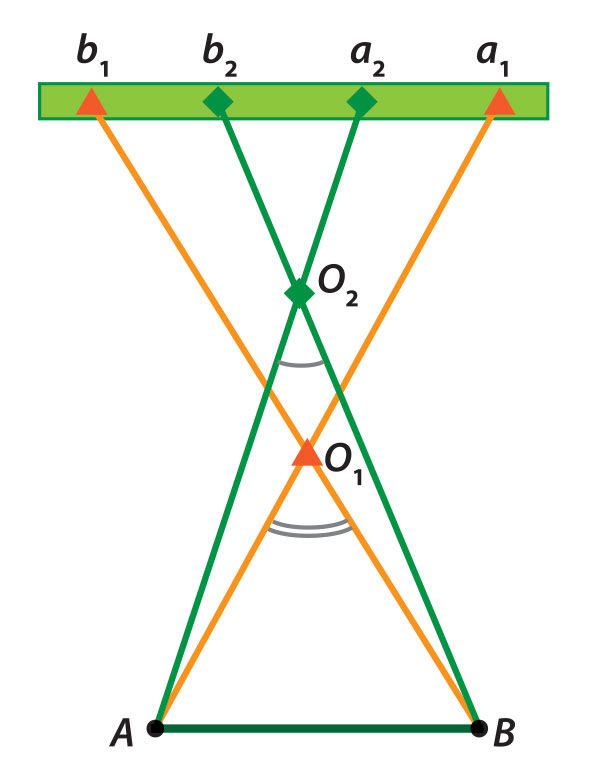
Kitas nuotolinis atstumų iki astronominių objektų nustatymo metodas – paralakso metodas. Tai seniausiai taikomas metodas atstumams iki dangaus kūnų nustatyti. Pirmiausia jis buvo pritaikytas atstumams Žemėje matuoti. Tarkime, kad stebime skirtingais nuotoliais esančius objektus O1 ir O2 iš taškų A ir B (2.7.1 pav.). Tolimo horizonto fone objektą O1 iš taško A matysime a1 kryptimi, o iš taško B – b1 kryptimi. Stebimų krypčių skirtumą nusako kampas AO1B, vadinamas paralaksù8. Jei žinome atstumą AB (vadinamą baze) ir išmatuojame kampus O1AB ir O1BA, galime apskaičiuoti objekto O1 atstumą nuo A arba B. Analogiškai skaičiuojamas atstumas nuo tolimesnio objekto O2. Iš brėžinio matome, kad paralakso dydis priklauso nuo stebėtojo atstumo iki objekto – tolimesnio objekto O2 paralaksas mažesnis už artimesnio objekto O1 paralaksą. Taigi, paralakso metodą galime taikyti atstumams matuoti nuotoliniu būdu.
8 Paralãksas [gr. παράλλαξις (parállaxis) – nuokrypa]
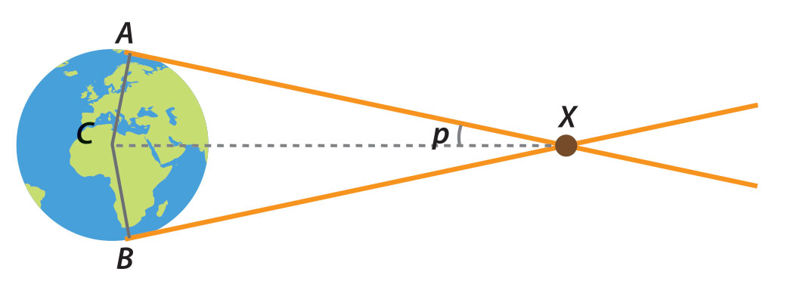
Žmogaus stereoskopinis regėjimas taip pat pagrįstas šiuo reiškiniu (bent jau tam tikru mastu). Astronominiams atstumams nustatyti reikia daug ilgesnių bazių nei atstumas tarp akių (apie 7 cm). Matuojant atstumus Saulės sistemoje tinkama bazė yra Žemės spindulys AC = CB = R⊕ (žr. 2.7.2 pav.). Tarkim, norime išmatuoti atstumą nuo Žemės iki Saulės sistemos objekto X. Tam tikslui turime iš matuoti objekto X koordinatès žvaigždžių atžvilgiu žvelgdami iš stebėjimo vietos A ir iš stebėjimo vietos B ir apskaičiuoti ∡AXC = p. Stačiojo trikampio CAX statmuo AX žymi vietos A horizonto liniją. Todėl kampas p vadinamas horizòntiniu paralaksù. Juo matomas Žemės spindulys, statmenas regėjimo krypčiai, žvelgiant iš objekto. Iš trikampio CAX apskaičiuojame atstumą iki objekto X:
. (2.7.2)
Šioje formulėje paprastai taikomas Žemės pusiaujinis spindulys
Saulės sistemos kūnų horizontiniai paralaksai nėra dideli. Pavyzdžiui, Mėnulio horizontinis paralaksas vidutiniu nuotoliu nuo Žemės lygus 57′, Saulės – 8,794″. Kai Venera ir Marsas būna mažiausiu nuotoliu nuo Žemės, jų horizontiniai paralaksai maždaug yra 31″ ir 23″.
Iš matematikos žinome, kad mažiems kampams galioja taisyklė sin α ≈ α. Čia kampas α turi būti iš reikštas radianais [rad]. Taikydami šią taisyklę ir paralaksą išreikšdami radianais (1 rad = 206 265″), gauname skaičiavimams patogesnę (2.7.2) formulės išraišką:
Žvaigždės yra nepalyginamai toliau nuo Žemės negu Saulės sistemos kūnai, todėl jų horizontiniai paralaksai neišmatuojamai maži. Norint aptikti žvaigždžių paralaksus, reikia matuoti žvaigždžių koordinatès iš skirtingų Žemės orbitos taškų, t. y. vietoj Žemės spindulio baze pasirinkti Žemės orbitos aplink Saulę spindulį. Tarkime, kad iš Žemės orbitos dviejų taškų A ir B fotografavome artimą žvaigždę Z tolimų objektų (žvaigždžių, galaktikų) fone (2.7.3 pav.). Kai Žemė buvo A taške, žvaigždės Z (raudonas taškas) padėtis tolimų žvaigždžių atžvilgiu buvo užfiksuota tokia, kokia pavaizduota dešiniajame kvadratėlyje ZA. Maždaug po pusmečio Žemė pasiekė priešingą orbitos tašką B, ir žvaigždės Z padėtis tolimų objektų atžvilgiu užfiksuota tokia, kokia pavaizduota kairiajame kvadratėlyje ZB. Palyginus žvaigždės Z padėtis šiose nuotraukose, galima įvertinti jos (paralaksinį) poslinkį tolimųjų objektų atžvilgiu. Tarkime, Žemė aplink Saulę skrieja apskritimine orbita, kurios spindulys SA = SB = a0 = 1 au (2.7.3 pav.). Atstumas nuo Saulės iki tiriamosios žvaigždės SZ = r. Tada kampas ∡AZS = π, parodantis žvaigždės Z poslinkį tolimųjų žvaigždžių atžvilgiu, vadinamas metiniu paralaksù, arba paralaksù.
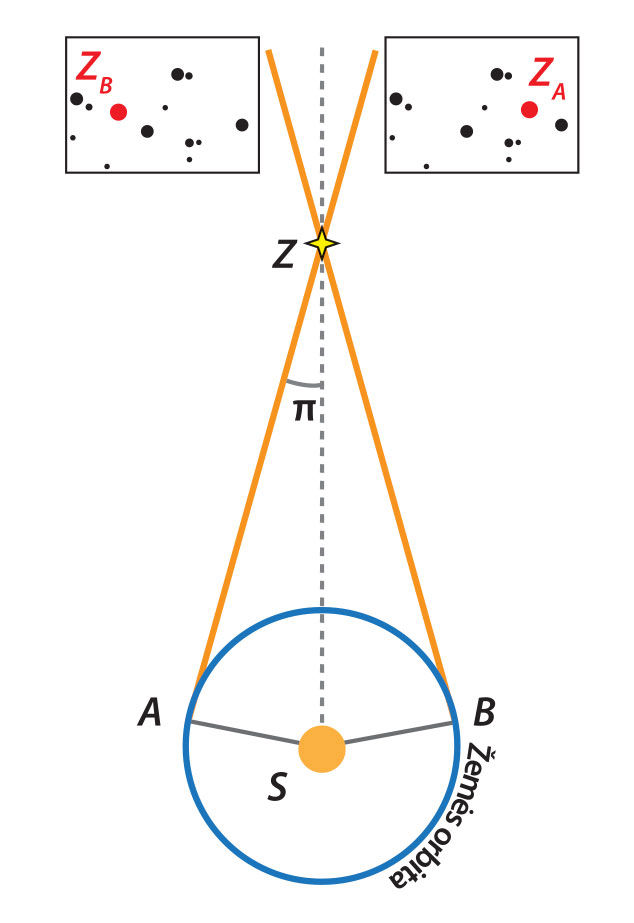
Žvaigždės metinis paralãksas yra kampas, kuriuo iš žvaigždės matomas Žemės orbitos 1 au ilgio spindulys, statmenas krypčiai „Žemė–žvaigždė“.
Didžiausią metinį paralaksą (0,768″) turi artimiausia Saulės sistemai žvaigždė – Kentauro Proksima. Visų kitų žvaigždžių paralaksai mažesni. Su Žemėje esančiais teleskopais žvaigždžių paralaksai išmatuojami 0,01″ tikslumu. Daug tiksliau paralaksai išmatuojami remiantis kosminių teleskopų stebėjimais. Pavyzdžiui, Europos kosmoso agentūros kosminiu teleskopu „Gaia“ paralaksai išmatuoti 0,0001″–0,00001″ tikslumu. Didžiausio regimojo spindesio žvaigždžių paralaksai pateikti vadovėlio priede.
Atstumą iki žvaigždės SZ apskaičiuojame iš trikampio SAZ (2.7.3 pav.):
Kadangi žvaigždžių metiniai paralaksai mažesni nei 1″, tai vėl galima pasinaudoti mažų kampų taisykle ir atstumą skaičiuoti pagal formulę:
Matome, kad, skaičiuojant žvaigždžių atstumus astronominiais vienetais, gaunami labai dideli skaičiai. Todėl buvo įvestas ilgesnis atstumo vienetas – parsèkas9, žymimas simboliu pc.
9 Parsèkas [angl. parallax + second ⭢ parsec – pc]
Vienas parsèkas yra nuotolis, kuriuo esančios žvaigždės (šviesulio) paralaksas lygus 1″.
Iš (2.7.5) formulės gauname:
Kai nuotolis matuojamas parsekais (pc), o para laksas sekundėmis (″), gauname paprastąjį šių dydžių sąryšį:
Kaip žinome, atstumai iki žvaigždžių ir galaktikų dar matuojami šviesmečiais (ly; žr. 1.2 posk.). Parseko ir šviesmečio sąryšis:
Klausimai ir užduotys
- Marso horizontinis paralaksas lygus 23″. Koks jo atstumas nuo Žemės astronominiais vienetais?
- Koks žvaigždės atstumas parsekais ir šviesmečiais, jei jos paralaksas lygus 0,0001″?
- Panagrinėkite žvaigždės paralakso reiškinį naudodamiesi programėle. Atsakykite į šiuos klausimus: kaip keičiasi žvaigždės paralaksas didėjant jos atstumui nuo Saulės? Kuriuose orbitos taškuose turėtų būti Žemė, kad žvaigždės paralaksinis poslinkis būtų didžiausias?
Astronominių objektų matmenų nustatymas
Jei žinome atstumą iki dangaus šviesulio, tai, išmatavę jo regimąjį kampinį skersmenį, galime apskaičiuoti ir jo tikrąjį skersmenį arba spindulį. Tarkime, tam tikru laiko momentu išmatavome šviesulio X regimąjį kampinį skersmenį θ ir atstumą r tarp šviesulio X centro ir Žemės centro T (2.7.4 pav.).
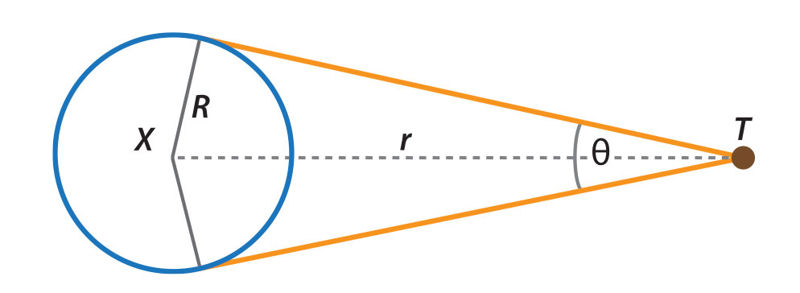
Tada šviesulio tikrasis spindulys
Jei šviesulių kampiniai matmenys maži ir išmatuoti kampinėmis sekundėmis, taikome mažų kampų taisyklę ir gauname:
Jei šviesulys yra Saulės sistemos objektas, kurio horizontinis paralaksas p išmatuotas sekundėmis, remiantis (2.7.2) formule jo tikrasis spindulys
čia R⊕– pusiaujinis Žemės spindulys.
Jei šviesulys yra už Saulės sistemos ribų, pavyzdžiui, žvaigždė, kurios metinis paralaksas π išmatuotas sekundėmis, remiantis (2.7.4) formule jos tikrasis spindulys bus lygus
čia a0 = 1 au.
Jupiterio atstumas ir matmenys
Uždavinys. Žinomi šie Jupiterio stebėjimų duomenys: horizontinis paralaksas p = 2,18″, regimojo disko kampinis skersmuo ties pusiauju θE = 48,9″, o skersmuo per ašigalius – θP = 45,7″. Apskaičiuokite Jupiterio atstumą nuo Žemės šių stebėjimų laiku (kilometrais ir astronominiais vienetais) ir Jupiterio linijinį spindulį ties pusiauju ir per ašigalius.
Sprendimas
Jupiterio atstumą apskaičiuojame pagal (2.7.3) formulę:
Jupiterio spindulį apskaičiuojame pagal (2.7.11) formulę. Jupiterio spindulys ties pusiauju:
Jupiterio spindulys per ašigalius:
Žvaigždės atstumas ir matmenys
Uždavinys. Žvaigždės paralaksas π = 0,2846″, o jos regimasis kampinis skersmuo θ = 0,00545″. Raskite žvaigždės atstumą ir spindulį. Palyginkite gautą spindulio vertę su Saulės spinduliu (R⊙= 6,957 ∙ 105 km).
Sprendimas
Žvaigždės atstumą apskaičiuojame pagal (2.7.7) formulę.
Žvaigždės spindulį apskaičiuojame pagal (2.7.12) formulę:
Klausimai ir užduotys
- Kai Venera buvo 77 milijonų km nuotoliu nuo Žemės, jos kampinis skersmuo buvo lygus 32,4″. Koks šios planetos tikrasis (linijinis) skersmuo?
- Arktūro paralaksas 0,0888″, kampinis skersmuo 0,021″. Apskaičiuokite jo atstumą parsekais ir linijinį spindulį kilometrais ir Saulės spindulio vienetais (R⊙ = 6,957 ∙ 105 km).
- Saturno horizontinis paralaksas 1,00″, jo kampinis skersmuo ties pusiauju 18,9″, o jį supančio žiedo išorinis skersmuo 42″. Apskaičiuokite Saturno atstumą nuo Žemės (kilometrais ir astronominiais vienetais), jo tikrąjį spindulį ties pusiauju ir išorinio žiedo spindulį.
- Planetiškojo ūko centre stebimos žvaigždės (baltosios nykštukės) paralaksas 0,0012″. Planetiškojo ūko regimasis kampinis skersmuo 3,3″. Raskite planetiškojo ūko atstumą (parsekais ir šviesmečiais) ir jo linijinį spindulį (kilometrais ir astronominiais vienetais).
- Pro Žemę praskriejančios kometos horizontinis paralaksas 13,2″, kometos galvos kampinis skersmuo 13″, o jos uodegos regimasis kampinis ilgis 7°. Apskaičiuokite kometos atstumą nuo Žemės (astronominiais vienetais), kometos galvos skersmenį ir jos uodegos mažiausią ilgį (uodega matoma projekcijoje į dangaus sferą) (pastaba: kometos uodegos ilgiui skaičiuoti netinka mažų kampų formulė.)
